 |
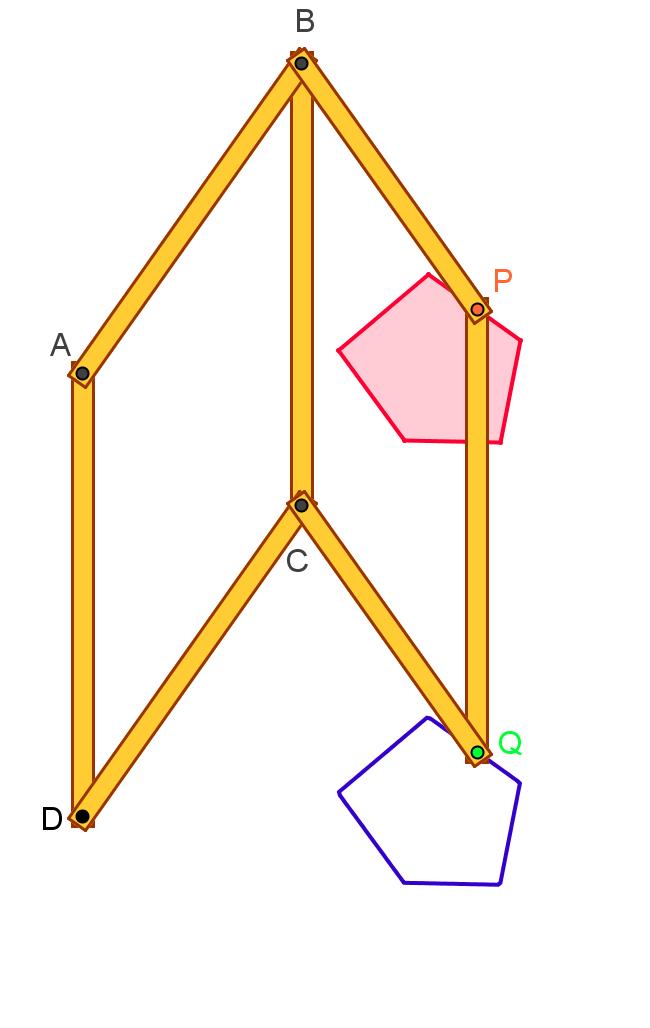 |
Il sistema è costituito da due parallelogrammi articolati aventi il lato CD in comune e giacenti sul medesimo piano .
Uno dei lati opposti a CD (per es. BA) è fissato al piano, l’altro è libero di muoversi (ha due gradi di libertà).
Infatti, scegliendo un punto sul piano e portando su di esso il vertice P (o Q) del sistema articolato, automaticamente il vertice Q (o P) individua il suo corrispondente nella traslazione caratterizzata in modulo, direzione e verso dal vettore BA (o AB). Originariamente utilizzato come servomeccanismo per disegnare segmenti paralleli ad un segmento dato (BA, CD, PQ sono sempre paralleli fra loro), lo strumento genera anche una particolare trasformazione geometrica (corrispondenza biunivoca tra due regioni diverse del piano).
Zona dei punti del piano accessibili al puntatore P
 |
Il sistema è costituito da due parallelogrammi articolati aventi il lato CD in comune e giacenti sul medesimo piano.
Uno dei lati opposti a CD (per es. BA) è fissato a p, l’altro è libero di muoversi (ha due gradi di libertà).
Il sistema articolato pilota l’asta PQ (PQ ha lunghezza arbitraria ), scegliendo un punto sul piano e portando su di esso il vertice P (o Q) del sistema articolato, automaticamente il vertice Q (o P) individua il suo corrispondente nella traslazione caratterizzata in modulo, direzione e verso dal vettore PQ (o QB).
 |
Nel modello fisico, le lastre rettangolari ∏ (trasparente) e ∏’ rappresentano due piani paralleli.
Il quadrilatero appartenente al piano ∏’ si può immaginare come ombra solare di quello appartenente al piano∏.
In generale, i raggi del sole (paralleli, rappresentati nel modello da fili tesi) stabiliscono una corrispondenza (prospettività con centro improprio) fra i punti dei piani ∏ e ∏’: ad ogni punto P di ∏ corrisponde in ∏’ la sua ombra P’.
La macchina permette di sovrapporre i due piani con moto continuo, mantenendoli paralleli e senza ruotarli uno rispetto all’altro: durante tale movimento anche i fili tesi (raggi) conservano il loro parallelismo.
Quando i piani sono sovrapposti la corrispondenza fra i loro punti P e P’ diventa una trasformazione geometrica piana che si chiama traslazione.


