 |
 |
La lemniscata di Bernoulli è il luogo dei punti il cui prodotto delle distanza da due punti fissi è costante ed uguale al quadrato della semidistanza fra i due fuochi.
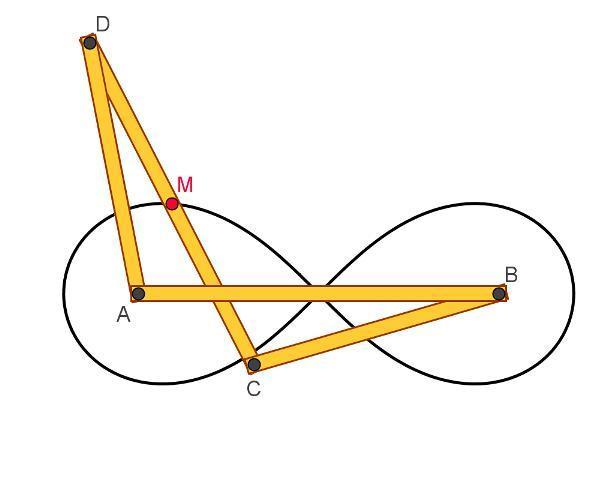
Nello strumento l'antiparallelogramma articolato ABCD, nel quale AB=AD√2 ha i vertici A e B fissati al piano del modello. Quando il punto D percorre la circonferenza di centro A, il punto C percorre la circonferenza di centro B e il punto medio M dell'asta DC descrive la lemniscata del Bernoulli.
La Lemniscata di Bernoulli è una particolare cissoide. Date in un piano due curve qualsiasi "C1" e "C2" ed un punto fisso A, si conduca per A una trasversale arbitraria che intersechi quelle curve rispettivamente in "P1" e "P2"; sulla trasversale si determini un punto P tale che sia (in valore assoluto e nel verso che procede dalla prima alla seconda curva) AP=P1P2: il luogo dei punti P si chiama Cissoide rispetto al polo A delle curve base "C1" e "C2"
Se le curve base coincidono in un’unica circonferenza si ha allora una Lemniscata del Bernoulli.


