 |
 |
Dalle “Cogitationes Privatae” e da una lettera a Beekman (ed. Adam-Tannery, vol. X: pagg. 156-158; 238-241) apprendiamo che nel 1619 Descartes realizza, oltre alla macchina per produrre medi proporzionali, anche un “compasso” per la suddivisione di un angolo in parti uguali .
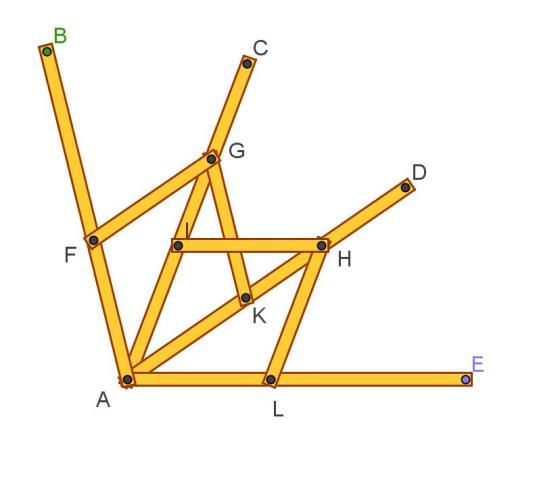
Come si vede dal modello fisico :
“Lo strumento è formato da quattro regoli, AB, AC, AD, AE, che hanno origine in A. I punti F, I, K, L sono equidistanti da A (cioè AF=AI=AK=AL) e i segmenti FG, GK, IH, LH, tutti uguali ad AF, possono ruotare intorno a F, I, K, L in modo tale che G possa muoversi lungo AC e H lungo AD. Per dividere in tre parti uguali un dato angolo α, occorre aprire il compasso fino a che l’angolo BAE sia pari ad α. Poiché i triangoli AFG, AKG, AIH, ALH sono sempre uguali, ne consegue che gli angoli corrispondenti FAC, GAD, DAE sono anch’essi uguali indipendentemente dall’ampiezza dell’angolo α. Perciò è sufficiente applicare il compasso a un angolo dato per dividerlo in tre parti uguali.
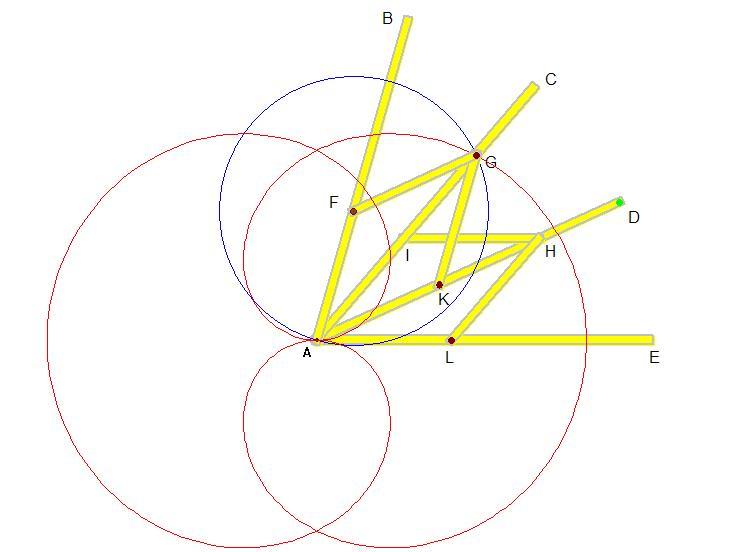
Possiamo anche tracciare la curva generata dal punto G quando il compasso viene aperto fino a far coincidere AE e AB con i lati dell’angolo dato α. Quindi, se tracciamo un cerchio di raggio FG intorno a F, l’intersezione fra questo cerchio e la curva individuerà il punto G per il quale passa la retta AC, che divide l’angolo secondo la proporzione di 2 ad 1. (Cfr. fig.2)
Descartes comprese immediatamente che l’aggiunta di una o più linee avrebbe permesso la divisione meccanica di un angolo in quattro o più parti…


