 |
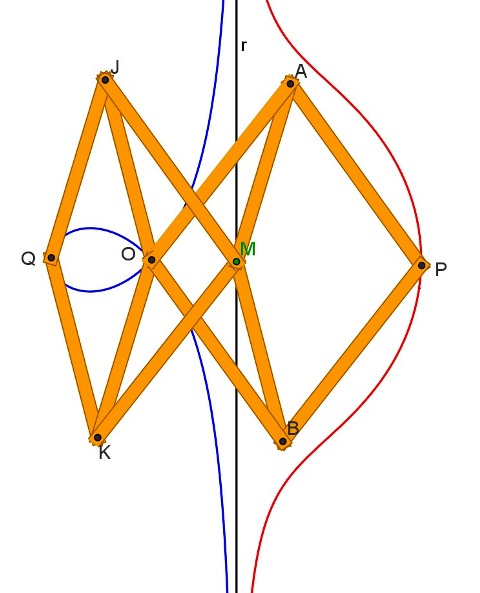 |
In una lettera a CH.Huygens datata 6 ottobre 1662, il matematico belga R.De Sluse (1622-1685) considera per la prima volta una cubica (circolare) avente un punto isolato: erano già noti esempi di cubiche nodate (Folium di Descartes) e cuspidate (Cissoide di Diocle). La cubica di De Sluse era da lui caratterizzata come segue: dato un punto O e una retta r si chiami M l’intersezione di questa con una trasversale condotta per O. Sulla trasversale si riporti, a partire da M e dalla parte opposta rispetto ad O, un segmento MP tale che risulti OM*MP=k2 . La curva descritta da P ha una forma che richiama quella della concoide di Nicomede: da qui il nome.
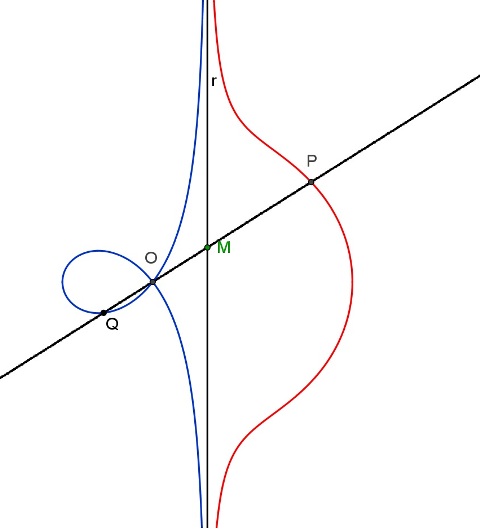
Se il segmento MP è riportato sulla trasversale, a partire da M, dalla stessa parte di O, si ottiene una cubica diversa dotata di nodo. Le due curve vengono indicate come concoidi slusiane .
Utilizzando l’inversione circolare e l’inversore di Peaucellier (1864) è facile ideare un meccanismo che tracci la curva “per moto continuo” in base alla sua originaria definizione.


