Trisettore di Pascal
 |
|
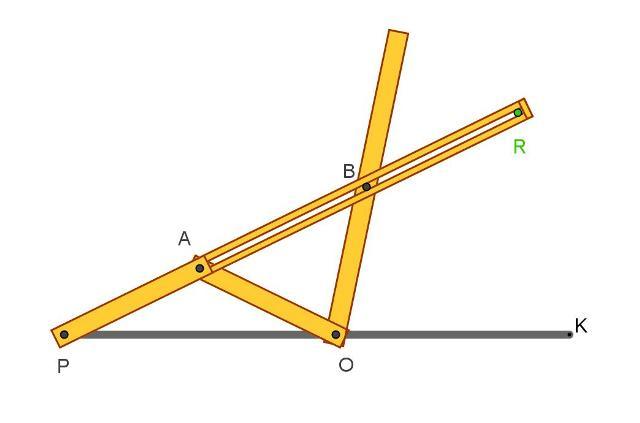
Per trisecare un angolo dato è quindi sufficiente far coincidere i suoi lati con OK e OB.
Considerato un piano π solidale con l’asta OB, il punto A descrive su di esso la circonferenza γ di centro O e raggio OB, l’asta PR passa sempre per B e il punto P (sull’asta) ha distanza costante da A. Il punto P descrive allora su π una lumaca di Pascal (curva trisettrice) che ha come circonferenza base γ, polo B e intervallo uguale ad OB (raggio della circonferenza base).Questo fatto giustifica il nome dello strumento.


