
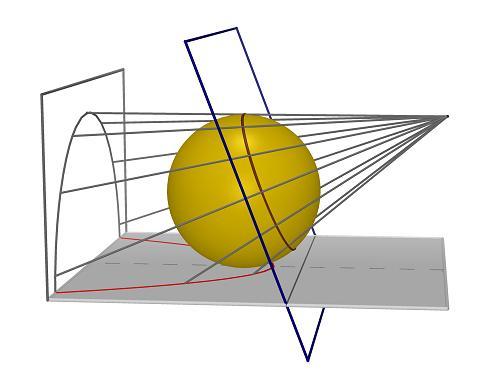
"Esistono due sfere iscritte in una superficie conica rotonda e tangenti ad un piano π(che la interseca e non passa per il vertice) se l’angolo θ della superficie conica (angolo acuto costante fra l’asse della superficie e una delle sue generatrici) non è uguale all’angolo φ formato dall’asse della superficie col piano π : in questo caso il piano π individua sulla superficie conica una ellisse oppure una iperbole. Se invece θ = φ(caso della parabola) esiste una sola sfera tangente a π. I punti di contatto delle sfere inscritte nella superficie conica e tangenti al piano πdella sezione si dicono fuochi della conica. Si chiama direttrice corrispondente ad un fuoco la retta comune a πe al piano che passa per il circolo di contatto della superficie conica con la sfera iscritta corrispondente al fuoco stesso. Quindi mentre ogni ellisse ed ogni iperbole ha due fuochi e due direttrici, ogni parabola ha un solo fuoco e una unica direttrice."
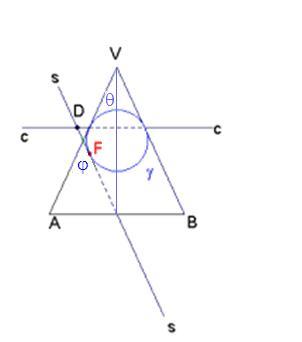
In figura VAB rappresenta il triangolo assiale, ottenuto tagliando il cono con un piano contenente l’asse. La circonferenza γ è l’ intersezione tra tale piano e la sfera di Dandelin. La retta cc è l’ intersezione tra il piano del triangolo per l’asse e il piano del circolo di contatto sfera-cono. La parte tratteggiata è il diametro del circolo di contatto. La retta ss è l’intersezione tra il piano del triangolo per l’asse e il piano della sezione conica. La parte di questa retta interna al triangolo è l’asse della parabola. F è il fuoco della parabola. Dal punto D si stacca (perpendicolarmente al piano del triangolo per l’asse) la direttrice della parabola.
Iperbole
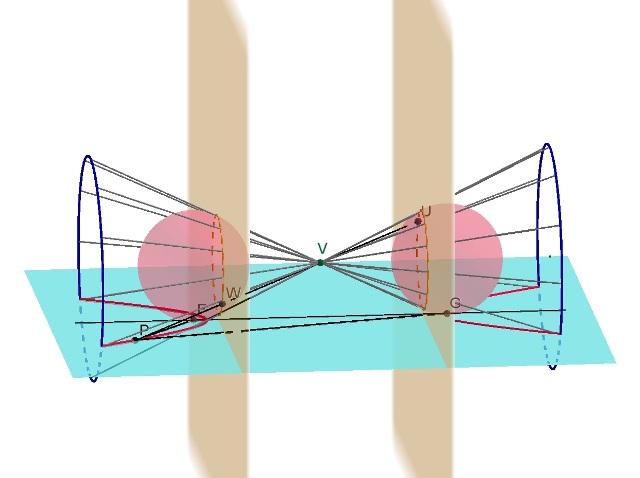
PG=PU (tangenti da P alla sfera)
PF=PW PG-PF=PU-PW=WU (costante)
Ellisse
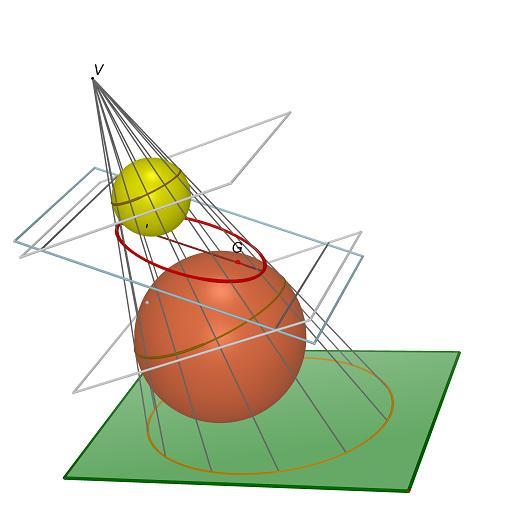
La conica, lungo cui un cono rotondo è segato da un piano, ha i fuochi nei punti ove il piano è toccato da sfere iscritte nel cono; direttrici della conica sono le rette intersezione tra il piano secante e il piano del cerchio di contatto sfera-cono (Dandelin - Quetelet, 1822). Nel caso della ellisse (rappresentato nel modello esposto) esistono due sfere siffatte: una di esse sta dalla banda del vertice rispetto al piano della conica, e l'altra dalla banda opposta. La definizione di fuoco d'una sezione del cono rotondo, che dal teorema si ricava, conduce (in base alle note proprietà delle tangenti condotte da un punto a una sfera) a stabilire, per via elementare, le principali proprietà dei fuochi di una conica. In una epoca in cui la maggior parte degli studi sulle coniche (in quanto curve generate entro lo spazio a tre dimensioni) viene effettuata nell'ambito della geometria proiettiva, Dandelin e Quetelet tornano per così dire alle origini, alle schematizzazioni proprie della geometria classica, ottenendo nuove proprietà, sfuggite all'attenzione dei ricercatori precedenti. Però, con una notevole differenza: benchè infatti l'enunciato del teorema sia "statico" (come il modello che lo illustra), le ricerche di Quetelet e Dandelin risultano legate alla geometria del movimento: precisamente allo studio delle "curve focali" (strofoidi), che sono quelle descritte dai fuochi di una ellisse quando il piano secante ruota attorno ad una delle due rette (in esso contenute) tangenti al cono.
In figura VAB rappresenta il triangolo assiale, ottenuto tagliando il cono con un piano contenente l’asse.
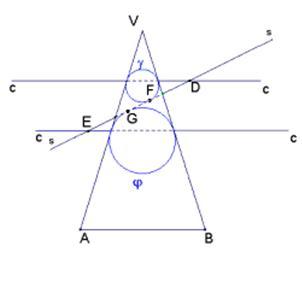
Le circonferenze Υ e φ sono le intersezioni tra tali piani e le sfere di Dandelin. Le rette cc sono le intersezioni tra il piano del triangolo per l’asse e il piano dei circoli di contatto sfera-cono (due in questo caso). Le parti tratteggiate sono i diametri dei circoli di contatto. La retta ss è l’intersezione tra il piano del triangolo per l’asse e il piano della sezione conica. La parte tratteggiata è l’asse maggiore dell’ellisse. F e G sono i fuochi dell’ellisse. Dai punti D ed E si staccano (perpendicolarmente al piano del triangolo per l’asse) le direttrici della ellisse relative ai fuochi


