
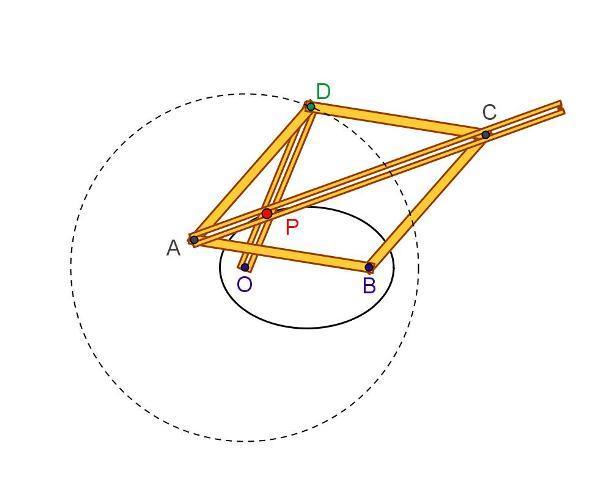
Il rombo articolato ABCD giace sul piano ∏ al quale è imperniato (in posizione prestabilita) il vertice B, mentre il vertice opposto D si muove, trascinato dalla manovella OD, lungo una circonferenza avente il centro fissato nel punto O di p, scelto in modo tale che sia OD = k > OB.
Si dimostra facilmente che P (punto di intersezione tra OD e AC) è equidistante da B e D, sicché OP + PB = OP +PD = OD = k. Quindi P descrive una ellisse avente O e B come fuochi.
Possiamo anche dire: in un piano ∏, il luogo dei punti P equidistanti da un punto fisso B e da una circonferenza di centro O e raggio assegnato k (contenente B al suo interno) è una ellisse.
Si chiama circonferenza direttrice di una ellisse (o iperbole) quella che ha il centro in uno dei due fuochi e raggio uguale all'asse principale della curva. Ellisse ed iperbole si possono definire come luogo (piano) dei punti equidistanti da un fuoco F e dalla circonferenza direttrice avente il centro nell'altro fuoco: nel caso della ellisse (illustrato nel modello esposto) il fuoco F è interno alla circonferenza direttrice, nel caso della iperbole esterno. L'enunciato vale anche per la parabola se si assume che la sua direttrice (linea retta) sia una circonferenza degenere di "raggio infinito" (si noti che la parabola si può considerare, secondo Euler, come una ellisse avente uno dei fuochi all'nfinito). E' opportuno ricordare qui i teoremi: a) Il luogo dei punti simmetrici di un fuoco di una ellisse o di una iperbole rispetto alle tangenti della medesima è il circolo direttore che ha per centro l'altro fuoco; b) Il luogo dei punti simmetrici di una parabola rispetto alle tangenti alla medesima è la direttrice.


