Alcune attività preliminari sono necessarie per evitare che nell’area semantica del termine “trasformazione”, quando viene usato nel linguaggio matematico, entrino immagini e significati derivanti dal linguaggio comune.
Per i matematici, si tratta di un termine tecnico non legato necessariamente né al tempo, né al movimento.
Siano date due regioni (figure) piane sovrapposte: i punti dell’una coincidano con i punti dell’altra, sicché le due regioni sono indistinguibili, identiche; per indicare coppie di punti sovrapposti si useranno notazioni del tipo (A, A’), (B, B’), ...ecc. (la presenza o l’assenza dell’apice individua la regione di appartenenza).
Una trasformazione è il risultato di un evento che ha separato le coppie inizialmente coincidenti, sicché i punti A, B, ...ecc. si trovano ora in posizioni diverse dai punti A’, B’ (corrispondenti od omologhi) benché i piani a cui le regioni inizialmente date appartengono siano ancora sovrapposti.
La nostra attenzione deve concentrarsi solamente sul risultato. Non importa quale evento si sia verificato, quanto tempo sia stato necessario: le due regioni vengono fotografate dopo che la trasformazione si è prodotta, e questa è caratterizzata dalle relazioni esistenti fra i punti omologhi (con lo stesso nome), cioè dalle proprietà della corrispondenza (biunivoca) fra i punti che sono rimasti immobili nella loro posizione iniziale e i punti prodotti dall’evento (immobili nella posizione finale). Se per separare i punti è stato usato un movimento o un’altra tecnica, ciò non ha alcuna importanza: il modo in cui la trasformazione è prodotta non interviene mai nella sua definizione (caratterizzazione).
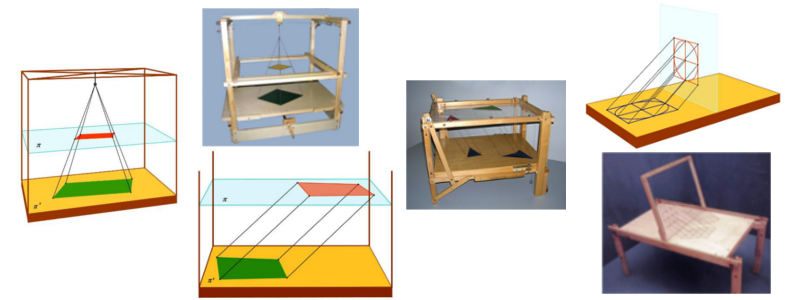
Meccanismi per trasformazioni. Fra le numerose tecniche per produrre trasformazioni prenderemo anzitutto in esame quella che si avvale di sistemi articolati o biellismi. Il meccanismo stabilisce una corrispondenza locale tra i punti di due regioni piane limitate sovrapposte collegandole fisicamente, e incorpora le medesime proprietà che caratterizzano la trasformazione. Lo studio dello strumento permetterà quindi di riconoscere il tipo di trasformazione che esso realizza: mentre il puntatore percorre una figura geometrica disegnata su una delle due regioni sovrapposte, il tracciatore disegna sull’altra la figura corrispondente (trasformata). Puntatore e tracciatore possono essere scambiati fra loro (biunivocità della corrispondenza). Oppure, il sistema articolato possiede due puntatori dotati ognuno di due gradi di libertà: non è nota alcuna figura iniziale, le figure che i puntatori disegnano contemporaneamente (le regioni che essi “ricoprono” durante il movimento) si corrispondono in una trasformazione.


