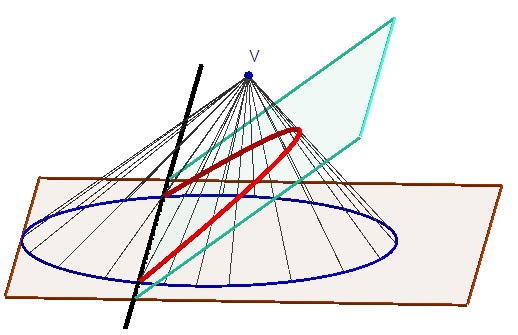Il modello fisico mostra come dalla prospettività in cui si corrispondono una circonferenza e una parabola si passa alla omologia che genera i punti della parabola partendo da quelli della circonferenza. Il movimento che trasforma gradualmente tale prospettività in omologia è proprio quello a cui pensava De la Hire nel suo trattato del 1673 e coincide con quello descritto nel teorema di Stevin.
Nella posizione “aperta” (figura a sinistra) il modello è identico a quelli che illustrano la teoria di Apollonio. Tuttavia qui è richiesta una lettura diversa del cono: le generatrici sono raggi che proiettano la circonferenza di base. 
Nella posizione “chiusa” (figura a destra), in cui si mette in evidenza, oltre al centro e all'asse della omologia il fascio dei raggi e una retta limite, si verifica l'allineamento dei punti corrispondenti con il centro di omologia.

  simulazione

Fonte: De la Hire, Nouvelle Méthode en Géométrie pour les sections des superficies coniques et cylindriques, Parigi 1673