 |
 |
Questa curva è di importanza fondamentale nella storia della matematica. Non risulta che essa sia stata presa in considerazione dai geometri dell'antica Grecia. Il suo studio fu condotto in modo approfondito solo nel '600 e nel '700: tutti i maggiori matematici dell'epoca si occuparono di essa e ne studiarono le proprietà. Le conoscenze su questa curva si sono sviluppate insieme a quelle sulla geometria analitica, sul calcolo infinitesimale, sul calcolo delle variazioni. Citiamo soltanto Galilei, Roberval (1646), Torricelli, Pascal (1658), Wallis, Huygens (applicazioni al pendolo), J.Bernoulli (problema della brachistocrona: 1696). Infine, nel 1847, Guillary dimostrò che la proiezione di un'elica cilindrica da un centro improprio su un piano opportuno è una cicloide.
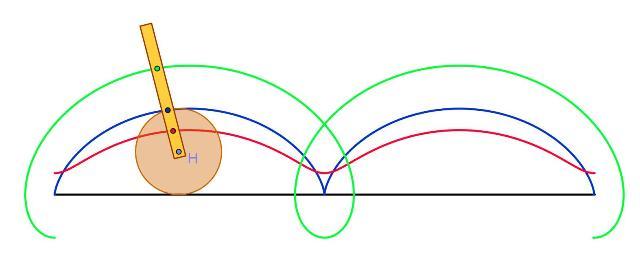
La cicloide è la curva descritta da un punto di una circonferenza la quale rotola senza strisciare su una retta che, per semplicità, possiamo immaginare orizzontale. Se il punto generatore sta sul bordo del cerchio si ha la cicloide ordinaria (cuspidata); se invece è interno al cerchio mobile si ha la cicloide accorciata; se è esterno si ha quella allungata (dotata di nodi). Notevoli i teoremi: 1) l'area sottostante ad un arco di cicloide ordinaria è tre volte l'area del cerchio generatore; 2) una massa pendolare che si muove lungo un arco di cicloide ordinaria compie oscillazioni con periodo indipendente dall'ampiezza (tautocronia della curva); 3) se una massa scivola senza attrito lungo una curva che congiunge un punto A ad un punto B sotto la sola azione della gravità, il tempo di discesa è minimo se la curva è un arco di cicloide ordinaria (la curva è brachistocrona).


