
Il Toro (Spira o Anello per i geometri del periodo greco-alessandrino) si ottiene dalla rotazione completa di un circolo attorno a una retta tracciata ad arbitrio nel suo piano.
I parametri che lo caratterizzano sono quindi due: il raggio r del cerchio generatore, la distanza d tra il centro di tale cerchio e l’asse di rotazione.
Le spiriche sono curve ottenute tagliando il Toro con un piano parallelo all’asse di rotazione; per caratterizzarle, oltre ai due parametri r, d già definiti ne occorre quindi un terzo: la distanza p tra l’asse del Toro e il piano secante.
la forma delle spiriche e delle cassiniame dipende in modo essenziale dalla forma del Toro (Spira, Anello) di provenienza. Precisamente:
1. Toro aperto (d > r).
Se ciò si verifica, spiriche e cassiniane sono costituite da due "ovali" una esterna all’altra (quando sia p < d-r); oppure da una sola "ovale" (quando d-r < p < d+r); infine (quando p=d-r) presentano un punto doppio.
2. Toro chiuso (d = r).
Se ciò si verifica, spiriche e cassiniane sono costituite da una unica "ovale" (p < 2r); nell’ipotesi p=2r si ha un punto doppio.
3. Toro rientrante (d < r).
Se ciò si verifica, spiriche e cassiniane sono costituite da due "ovali" una interna all’altra (quando p < r-d); oppure da una unica "ovale" (quando r-d < p <r+d); presentano infine un punto doppio se p = r-d o se p = r+d.
Esplora (caso del toro aperto)
Strumento del Delaunay per tracciare le spiriche
 |
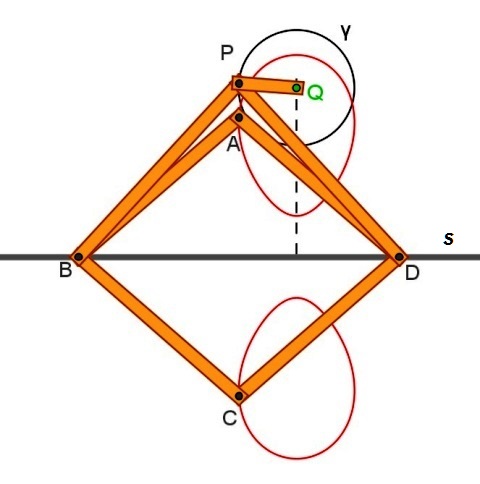 |
Il rombo articolato ABCD (di lato AB=a) ha i vertici B e D scorrevoli in una scanalatura rettilinea s. Le aste PA e PB di ugual lunghezza b (b>a) hanno due dei loro estremi incernierati in P; gli altri due estremi sono invece incernierati in B, D e scorrono anch'essi lungo la scanalatura s. P è vincolato (dall'asta QP imperniata al piano in Q) a percorrere una circonferenza γ . Quando P percorre γ , i punti A e C, insieme, descrivono una quartica corrispondente di γ in una trasformazione non lineare E' possibile variare la distanza di Q da s, ottenendo così Cassinoidi di forma diversa, composte da due ovali distinti, da un'unico ovale e come caso particolare, quando la distanza di Q da s è uguale a √((b2-a2) -r (r=raggio della circonferenza ) si ottiene una lemniscata. Le curve tracciate dalla macchina si possono ottenere come sezioni di un toro con piani paralleli all'asse


