A torus, also called spiral or ring in the classical Greece, is a revolutionary surface obtained by revolving a circle about a straight line drawn in an arbitrary position on the same plane of the circle.
A torus is therefore defined by the radius r of the generating circle and the distance d between the center of the circle and the axis of rotation.
By cutting a Torus with a plane parellel to the axis of rotation a spiric section is obtained. To define this curve, together with parameters r and d previously introduced, the distance p between thr Torus axis and the secant plane is needed.
The shape of the spirics and of the Cassini\'s curves strictly depends on the shape of Torus (also called Spiral or Ring) being sectioned. More precisely:
1. Ring torus (d>r)
In this case spirics and Cassini\'s curves can either appear as a couple of ovals one inside the other (p<d-r), a single oval (d-r<p<d+r) or a double point (p=d-r).
2. Horn torus (d=r)
In this case spirics and Cassini\'s curves appear as a single oval (p<2r) or a double point (p=2r).
3. Spindle torus (d<r)
In this case spirics and Cassini's curves can either appear as a couple of ovals one inside the other (p<r-d), a single oval (r-d<p<r+d) or a double point (p=r-d or p=r+d).
Strumento del Delaunay per tracciare le spiriche
 |
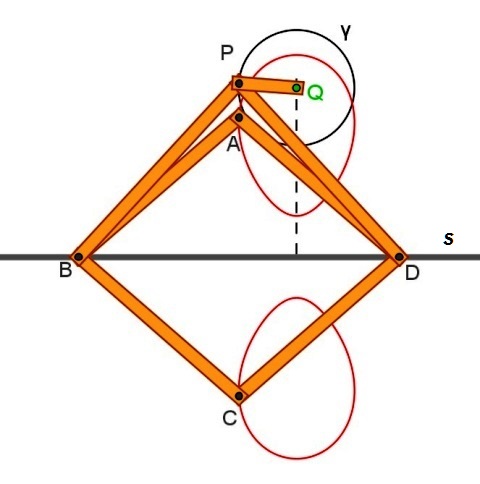 |
ABCD is an articulated rhombus with side AB=a and vertexes B and D forced to slide along the straight groove s. Rods PA and PB, linked in P, are the same length b, with b>a. Rod PQ is fixed to the wodden plane in point Q and forces P to draw circle y. When P moves along y , A and C together draw a quartic curve corresponding to y in a non-linear transformation. Varying the distance between Q and s Cassini\'s curves made of one or two ovals can be obtained. As a special case, the Leminscate is obtained when the distance between Q and s equals √((b2-a2) -r (r=radius of the circumference). All the curves traced by this machine can by secting a torus with plans parallel to its axes.