
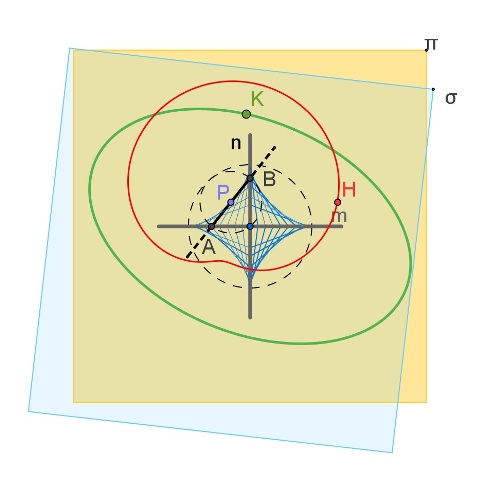
Si consideri un piano π sul quale siano incise due scanalature ortogonali m ed n intersecantisi in O. Un secondo piano σ (sovrapposto a π ) è rigidamente vincolato a un’asta AB (di lunghezza prefissata b) i cui estremi sono costretti - da appositi cursori - a scorrere entro le scanalature m ed n. Valgono i seguenti teoremi: 1) Se σ, guidato dall’asta AB si muove su π (tenuto fisso) ogni suo punto descrive (su π) una ellisse (il punto medio di AB descrive una circonferenza di centro O) 2) Durante il movimento descritto in 1) il segmento AB inviluppa una curva a quattro cuspidi (asteroide retta). 3) Se σ viene tenuto fisso e π guidato dalle scanalature m, n costrette a passare per A e B (che ora sono perni) , si muove su π, ogni suo punto descrive (su σ) "lumache" del Pascal (il punto O descrive una circonferenza di diametro AB). Gli stessi movimenti qui considerati si possono ottenere facendo rotolare senza strisciare (l’una sull’altra) una circonferenza di diametro AB (passante per O, fissata a σ ) e una circonferenza di centro O e raggio AB (fissata a π).


