|
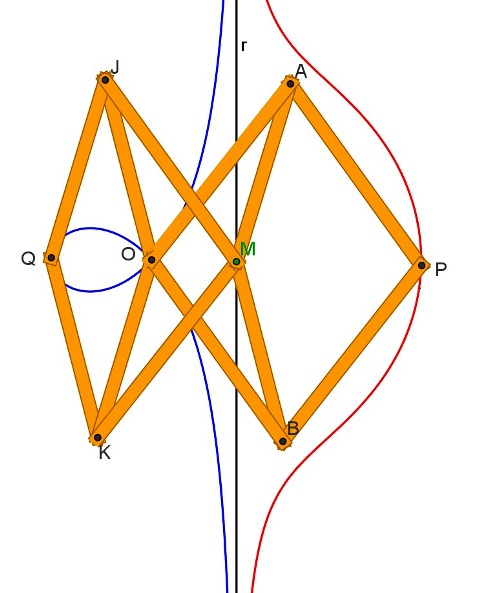 |
Whether knotted (Descartes\' folium) or cusped (Diocle\'s cissoid) cubic curves where known, a cubic curve was firstly mentioned by the Belgian mathematician R.De Sluse (1622-1685) in a letter to CH.Huygens dated October 6th 1662. This curve was defined by De Sluse as follows: given a point O and a straight line r, M is the intersection point between r and any line (t) throug O. On line t, opposite to M respect to O, the point P is considered, so that OM*MP=k2. Point P describes a curve similar to the Nicomede\'s conchoid and this is where the De Sluse\'s conchoid\'s name comes from.
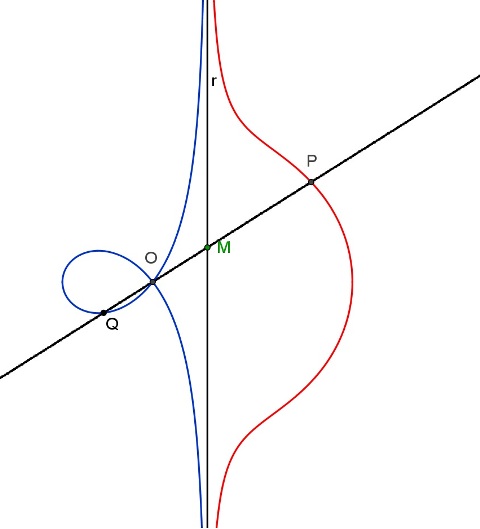
If on t MQ is considered, opposite to MP respect to M and so that MQ=MP, then point Q describes a knotted cubic curve. This curve, together with the one described by P, form the De Sluse\'s conchoid.
A mechanism tracing the curve based on the original definition using a continuous movement can easily be built by means of the circular inversion and the Peaucellier\'s inverter (1864).