 |
 |
La "scoperta" della cissoide risale al 200 a.C. circa, ed è dovuta a Diocle. Ce ne dà notizia Eutocio, in una celebre nota del suo commento al secondo libro del trattato di Archimede "Sopra la sfera e il cilindro", dove spiega come la curva fosse utilizzata per risolvere il problema dell'inserzione di medie proporzionali fra grandezza date. Nell'antichità era considerata come curva finita: l'esistenza dei rami infiniti fu avvertita solo verso la metà del '600. La generazione della cissoide con moto continuo risale a Newton ("Arithmetica Universalis", 1707). Numerosi studi sulla curva furono svolti nella seconda metà dell'800.
La definizione di strofoide è una curva che troviamo presa in considerazione anche da Torricelli e da Roberval (1645). La generazione con moto continuo (mediante l'uso di una squadra, come per la cissoide) risale a Newton. Le strofoidi furono studiate da G. Casali nel 1757, e successivamente dal Quetelet (1819) e dal Dandelin (1822), che le hanno strettamente collegate ai fuochi delle coniche (chiamandole anche "curve focali").
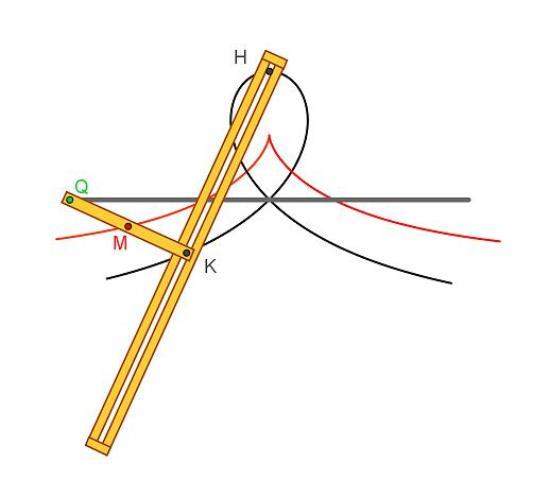
Lo strumento (squadra di Newton) è costituito da due aste QK e KH saldate in K ad angolo retto. All’estremità Q dell’asta QK è fissato un perno che scivola in una scanalatura rettilinea scavata sul piano π nel quale lo strumento giace. Un secondo perno H è fissato su π e l'asta KH (dotata di scanalatura) è costretta a passare per il perno H. Quando l’asta si muove su π il vertice K dell’angolo retto descrive una strofoide (retta), mentre il punto M del segmento QK traccia una cissoide .


