
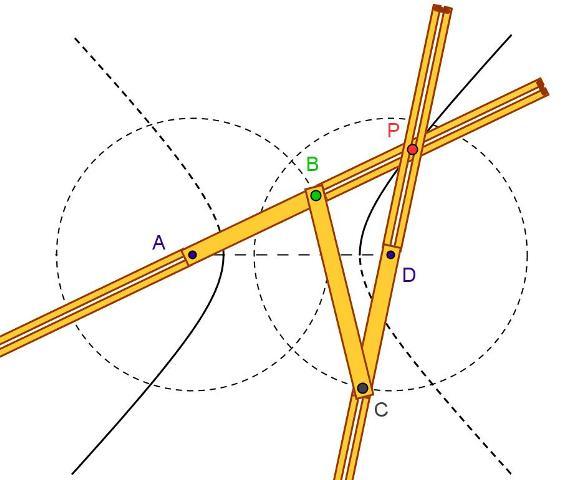
Tool drawing a hyperbola by means of an antiparallelogram
An atiparallelogram linkage is an articulated quadrilateral ABCD where the opposite sides, AB and CD, are the non-parallel sides of an isosceles trapezoid; the remaining two side, AD and BC, are the diagonals of the same trapezoid.
If the antiparallelogram is placed on a plan ∏, one of the two shortest sides (for example AB) blocked on ∏ and side BC moved on the plan, it can easily be inferred that C and B describe two circumferences with centers in D and A respectively. When properly extended sides AB and CD cross in P.
Because P belongs to the axis of symmetry of the antiparallelogram it is PA – PB = PA – PD = AB = cost. Therefore the set of points described by P is an arc of a hyperbola with A and D as focal points.
Iperboli che rotolano senza strisciare

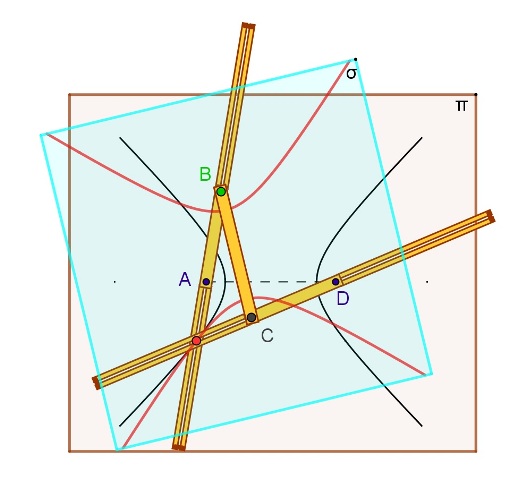
Uno dei lati maggiori (AD) dell'antiparallelogramma ABCD è fissato al piano del modello π,e l'altro (BC) è fissato ad un piano di plexiglas σ,sovrapposto a π e mobile rispetto a questo. Il punto P, intersezione delle aste prolungamenti di AB e CD descrive sul piano π una iperbole ξ di fuochi A e D , e sul piano σ una iperbole ξ' di fuochi C e D, uguale a ξ. Le due iperboli, durante il moto relativo dei due piani, rotolano l'una sull'altra senza strisciare e il punto P è, in ogni posizione, il loro punto di contatto.


