
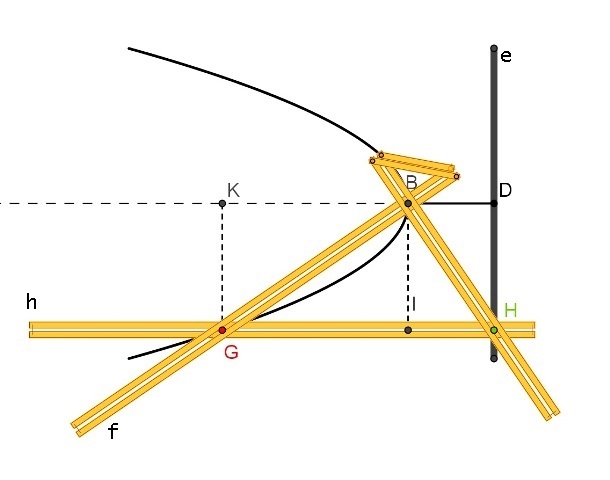
Il punto H scorre nella scanalatura e trascina nel suo movimento l’asta scanalata h , che rimane sempre perpendicolare ad e. Le due aste scanalate HB ed f sono vincolate a passare per il punto fisso B e formano un angolo retto in B. Quando H si sposta, h trasla , mentre HB ed f ruotano attorno a B. Durante il movimento il punto G, intersezione delle aste h ed f, descrive una parabola. Infatti:
valgono le seguenti uguaglianze: HI=DB , IG=BK e GK=IB. Dal triangolo rettangolo HBR si deduce :
BI2= HI∙IG, quindi GK2=DB∙BK.
Ponendo KG=y, BK=x e DB=k , la relazione precedente diventa y2=kx


