
Nel libro II° della "Geometria", Cartesio propone un metodo generale per trasformare una curva assegnata in un'altra di "genere" più elevato. (Si noti che il termine "genere" usato da Cartesio per classificare le curve, non ha lo stesso significato che ad esso viene attribuito attualmente in geometria: Cartesio raggruppa nel "genere" n-esimo le curve la cui equazione ha grado 2n oppure 2n-1). Il metodo è il seguente: Sia data, nel piano π , una curva C e un punto S ad essa rigidamente fissato. Sia inoltre G un punto fisso di π . La curva C sia assoggettata ad una traslazione su π : per ogni sua posizione, se ne determinino le intersezioni con la corrispondente posizione della retta SG. Il luogo geometrico di tali intersezioni è una nuova curva, trasformata di C.
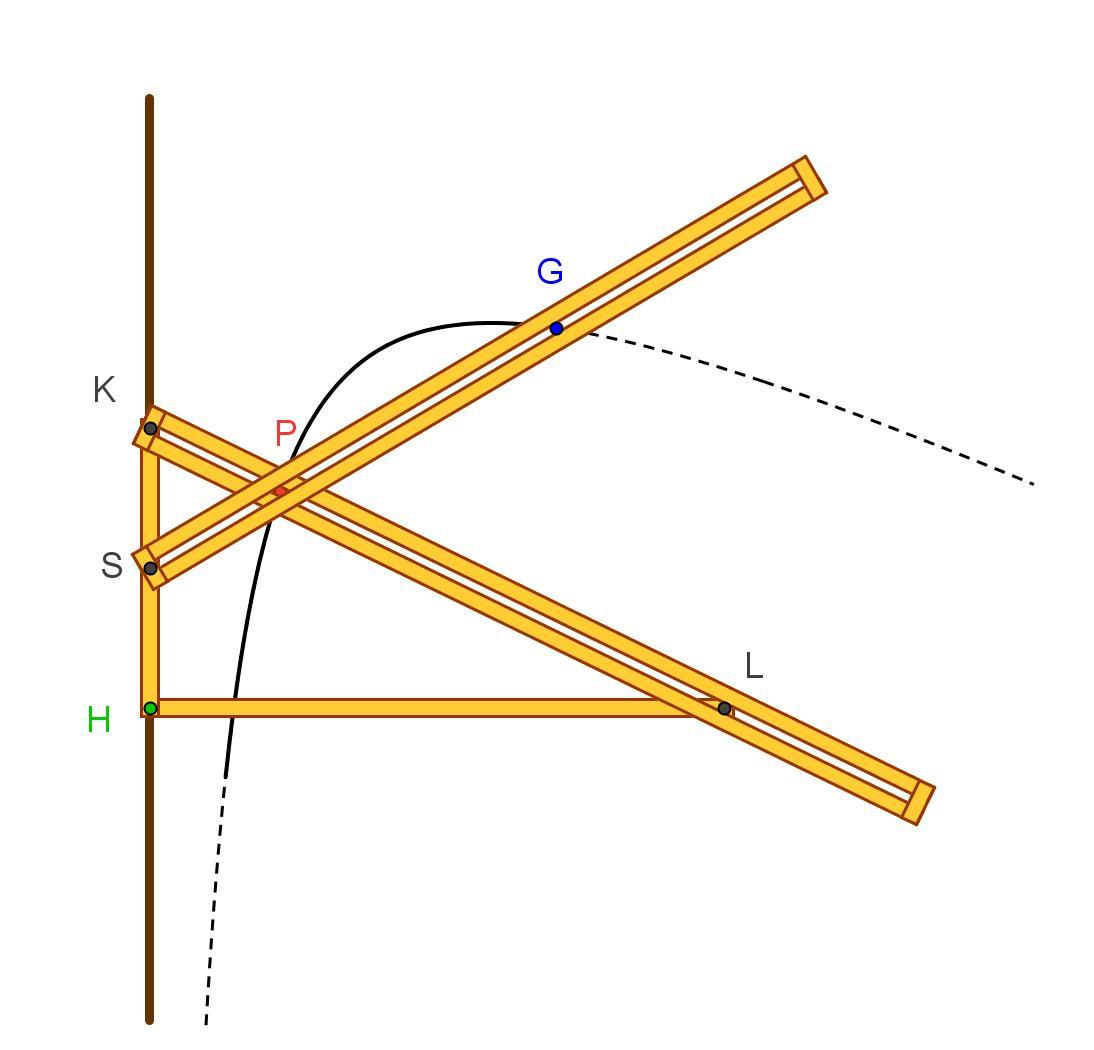
Nel modello esposto il cursore KH scorre nella scanalatura rettilinea r trascinando con sé (nel piano π) la retta KL e il perno S (KS = costante). In S è agganciata una retta SG costretta a passare per il perno G, fissato su π esternamente alla scanalatura r. Quando S si muove, SG ruota attorno a G mentre la retta KL trasla, formando con r un angolo di ampiezza costante. L’intersezione P tra SG e KL traccia una iperbole.
Se la curva C pilotata dal cursore KH non fosse una retta, ma ad esempio una parabola (dimensione 2), si otterrebbe dall'intersezione tra quest'ultima e la retta GS una cubica (tridente di Cartesio).


