 |
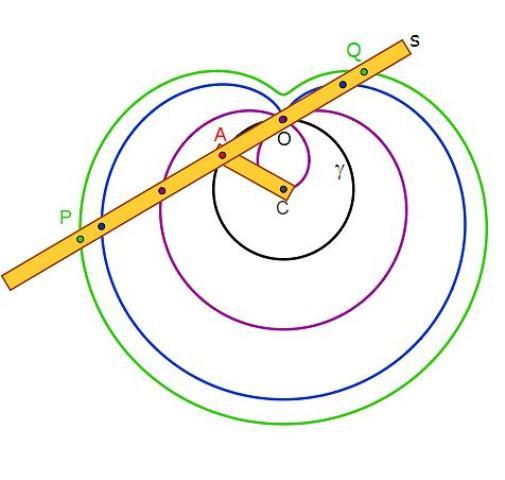 |
Il punto A è vincolato dall'asta AC=r, imperniata al piano in C, alla circonferenza γ di raggio r. L'asta s, incernierata in A alla CA , è vincolata a passare per un punto fisso O del piano, scelto sulla circonferenza γ.
Quando A descrive γ (circonferenza base), ognuno dei punti P e Q scelti su s in modo che siano simmetrici rispetto ad A, descrive una lumaca di Pascal, che presenta in O (polo) un punto doppio isolato, un nodo o una cuspide se risulta rispettivamente AP>2r, AP<2r o AP=2r.
Si possono dimostrare i teoremi:
1) le lumache del Pascal sono podarie di una circonferenza rispetto a un punto del suo piano ;
Costruzione del Durer
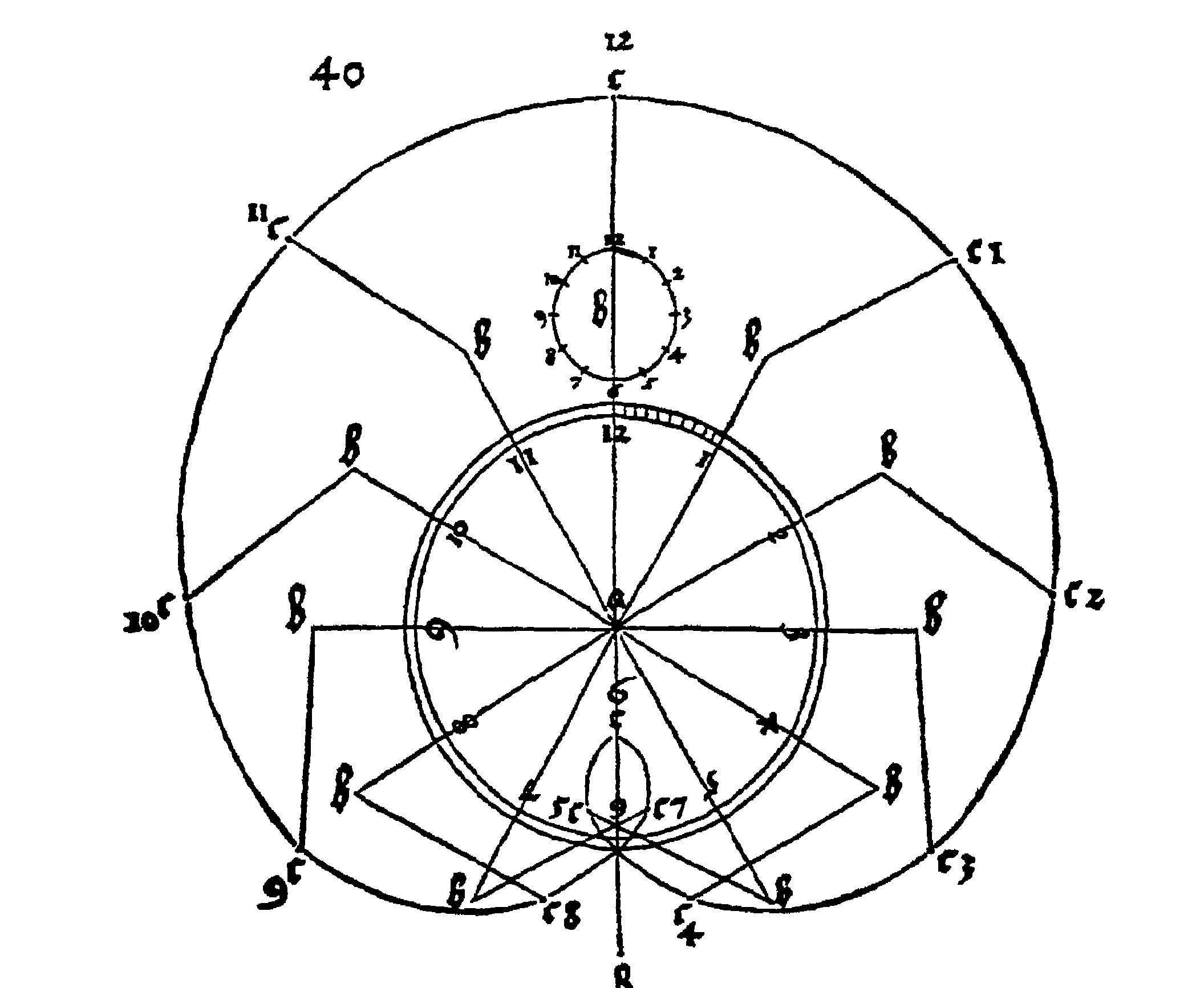
Si tracci una circonferenza e la si divida in 12 parti, ogni parte venga numerata come i numeri dell’orologio.
Si traccino i raggi per i punti di divisione e dalle estremità dei raggi per i punti 1,2, 3, ….. si traccino i segmenti uguali e paralleli ai raggi per i punti 2,4,6…. La curva passante per le estremità degli ultimi segmenti tracciati è una lumaca.
Dürer dà l’indicazione di dividere la prima “ora” in dieci parti, per tracciare altri punti della curva .
Bibilografia: J.L.Coolidge , The Mathematics of great amateurs, Dover Publications, Inc, 1963
E.H.Lockwood, A book of curves , Cambridge University Press 1961


