Concoide del Dürer
 |
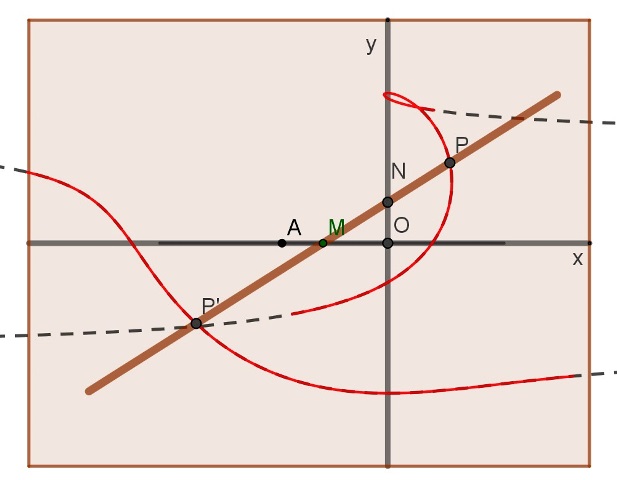 |
Lo strumento è costituito da un’asta imperniata in M ad un cursore vincolato a scorrere nella scanalatura Ox; un cursore, scorrevole entro l’asta stessa, è vincolato a muoversi lungo la scanalatura Oy. Due tracciatori P e P’ sono fissati sull’asta a ugual distanza b da M.
Sia A (-a,0) un punto sull’asse Ox e sia N il punto di intersezione dell’asta con l’asse Oy Un sistema di fili collegati ai due cursori, consente il movimento dell’asta in modo tale che sia sempre AM=ON. I punti P e P’ descrivono la concoide di Dürer. Equazione della Concoide (xy+b2 -y2-)2 =(x+y-a)2(b2-y2)
Albert Dürer descrive la curva da lui chiamata “Muschellinie” nel suo trattato “Underweysung der Messung mit dem Zirckel und Richtscheyt”(1525).
“Desidero tracciare anche un’altra curva, che potrà servire in numerose circostanze. Procedo come segue: Traccio una linea orizzontale di primo estremo a e secondo estremo b. Iniziando a contare da a segno su questa linea 16 punti equidistanti, curando che tra il punto 16 e il secondo estremo b rimanga un segmento di lunghezza arbitraria. Poi dal punto 13 elevo, sulla orizzontale ab, una verticale di lunghezza uguale al segmento che ha come estremi i punti a,16. Traccio su questo segmento una graduazione come la precedente (che lo divida quindi in 16 parti uguali) contando dal basso verso l’alto. Prendo una riga: segno su di essa un segmento di lunghezza ab, e la sistemo in modo tale che una estremità a di questo segmento ab coincida con il punto 1 della retta orizzontale, mentre il bordo della riga passa per il punto 1 della verticale. Attribuisco il contrassegno 1 anche al punto in cui si trova in tal caso l’altro estremo b del segmento ab disposto sulla riga. Di seguito: appoggio la riga in modo che l’estremità a del segmento ab che esso sostiene si trovi in 2 alzandola sulla verticale fino a 2 e attribuendo il numero 2 al punto in cui va di conseguenza a collocarsi l’estremo b. Procedendo allo stesso modo per tutti i punti delle linee orizzontale e verticale fino a 16. Congiungendo i vari punti così ottenuti si ottiene una linea a forma di conchiglia (Muschellinie)”


