La cissoide (a quanto riferisce Eutocio nel Commento all'opera di Archimede), fu ideata e usata dal geometra greco Diocle per duplicare il cubo o, più generalmente, "per inserire fra due date rette due medie proporzionali" (il termine "retta" ha qui il significato che noi attribuiamo a "segmento").

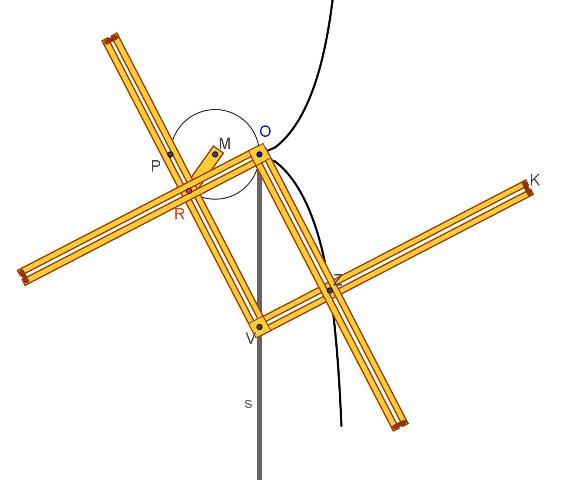
Lo strumento è costituito da:

• una squadra ROZ avente il vertice O imperniato su un piano e il lato OR dotato di una scanalatura rettilinea costretta a scivolare lungo un cursore R, vincolato a sua volta all’estremo R dell’asta MR che descrive una circonferenza passante per O (diametro OP, centro M);

• una seconda squadra RVK, collocata nel medesimo piano della prima, il cui vertice V percorre una scanalatura rettilinea s passante per O e perpendicolare al diametro PO, mentre il lato VR (anch’esso scanalato) è vincolato a scorrere lungo il cursore R e a passare per il perno P

Quando R percorre la circonferenza di centro M passante per O il punto Z, intersezione degli altri due lati delle squadre, descrive una cissoide.

 Esplora la macchina

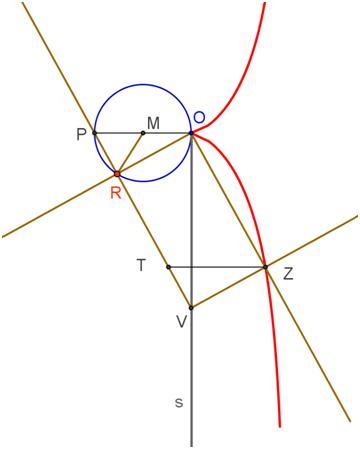
Si tracci da Z la perpendicolare ad OV che interseca VP in T. I triangoli OPR e ZVT sono congruenti quindi VT=PR. Al variare di R sulla circonferenza C di centro M e diametro OP, T descrive la cissoide avente come base la circonferenza C. Poiché POZT è un parallelogramma, ZT è equipollente a OP e i punti Z e T si corrispondono in una traslazione; anche Z descrive una cissoide avente come base la circonferenza traslata della C nella traslazione di vettore PO.

Osservazione: quando V percorre la retta s, e il lato PV della squadra è costretto a passare per il punto fisso P l'altro lato della squadra inviluppa una parabola avente P come fuoco ed s come tangente nel proprio vertice: il punto Z quindi descrive la podaria di questa rispetto al vertice O.

animazione