Simmetria assiale ortogonale
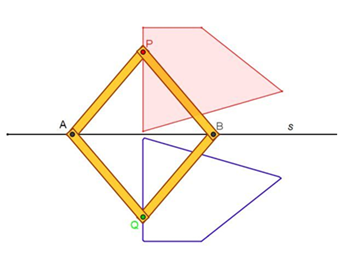Un rombo articolato ha
due vertici opposti vincolati a cursori che scorrono entro una scanalatura
rettilinea s.
Il biellismo ha due gradi di libertà:
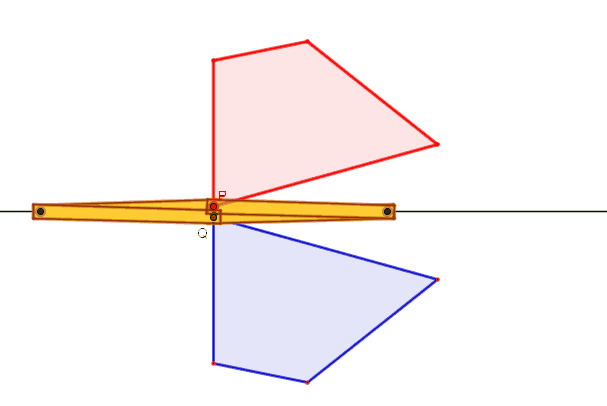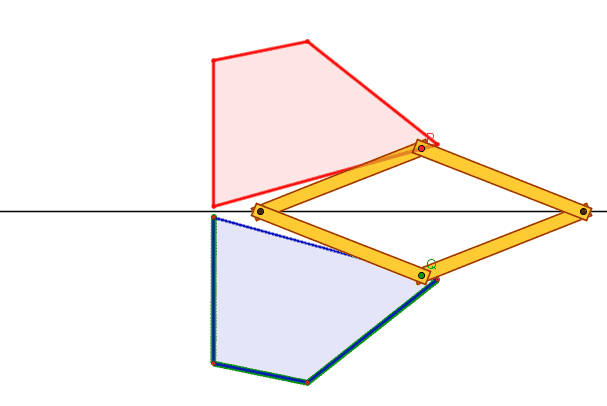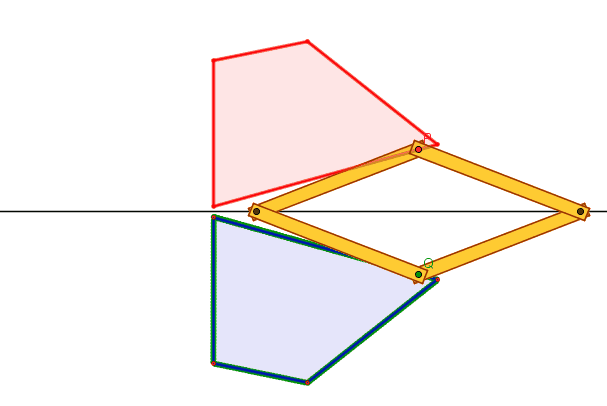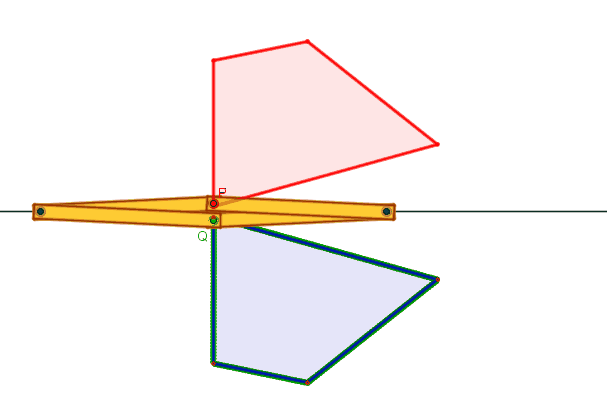
i vertici liberi del rombo (P e Q) descrivono perciò due regioni piane
(limitate) che si trovano in semipiani opposti aventi s come origine comune. La
posizione di P determina univocamente quella di Q (e viceversa).
Dalla semplice geometria del sistema
meccanico si ricava subito che:
la retta PQ è perpendicolare ad s;
i punti P e Q sono equidistanti da s.
Perciò P e Q si corrispondono nella
simmetria assiale ortogonale di asse s.
Se (per es.) P è vincolato a una
traiettoria assegnata, Q descrive la traiettoria simmetrica rispetto ad s.
