|
|
|
|
|
|
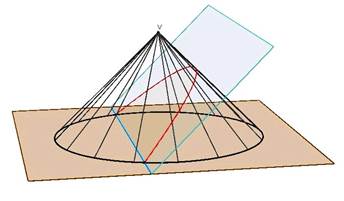
Cono
di Menecmo
La teoria delle coniche, la cui scoperta è attribuita
a Menecmo (discepolo di Eudosso
e fratello di Dinostrato, vissuto tra il 375 e il 325
a. C.) si sviluppò nella seconda metà del IV secolo a. C.: trattati specifici
(dovuti ad Aristeo ed a Euclide) comparvero solo attorno al 300 a. C. Per gli
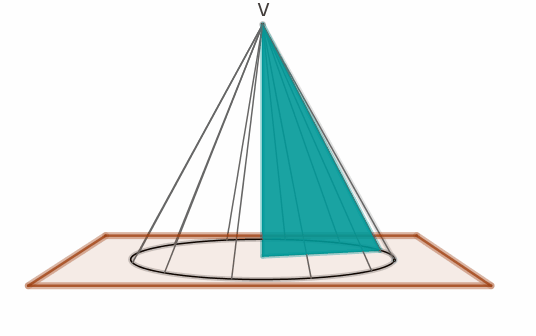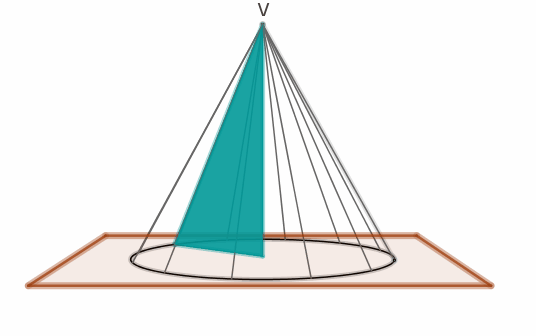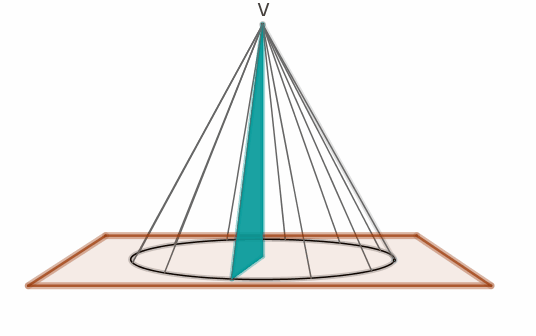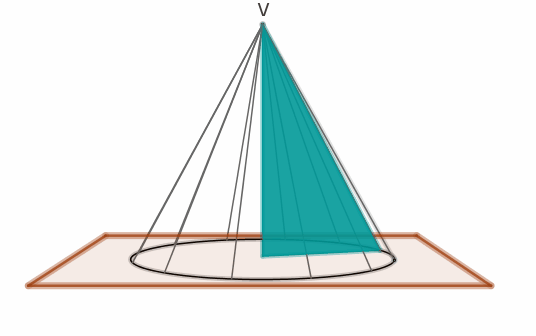
antichi, coni erano i solidi generati da un triangolo rettangolo rotante
attorno ad uno dei cateti (cioè coni circolari retti) e li classificavano in
coni rettangoli, ottusangoli o acutangoli a seconda del tipo di angolo formato
nel vertice di una sezione meridiana completa; infine usavano ciascuna specie
di cono per generare un solo tipo di conica tagliando ogni cono con un piano
perpendicolare ad una generatrice. Ogni conica veniva caratterizzata attraverso
il “sintomo”: una proporzione che legava i loro singoli punti al cono di
appartenenza. La deduzione del sintomo (al quale veniva poi ricondotta ogni
altra proprietà della curva) era fatta nello spazio a tre dimensioni: perciò
alle coniche, benché giacenti sul piano secante, veniva riservata dagli antichi
la qualifica di “curve solide”.
A cura
dell'Associazione Macchine Matematiche
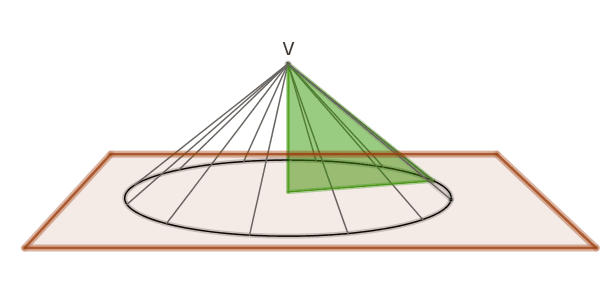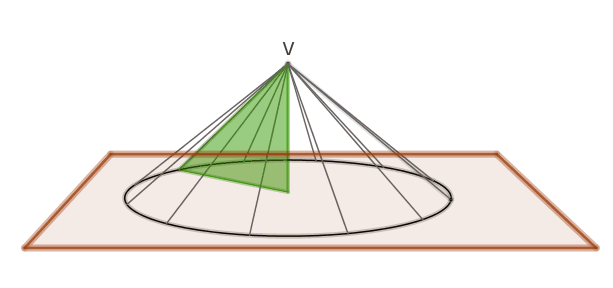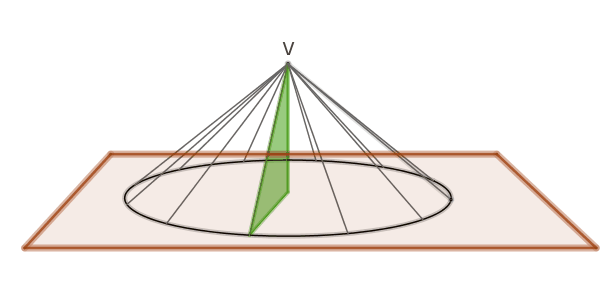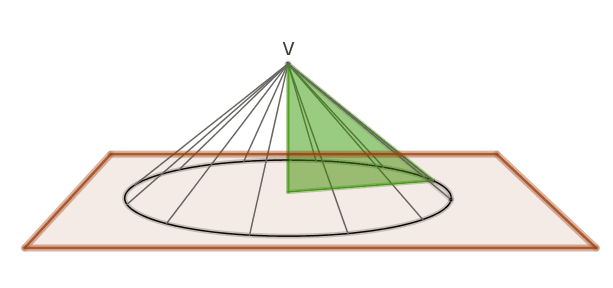
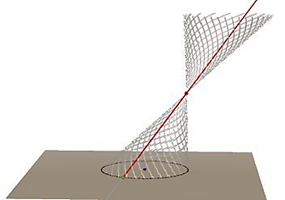
Apollonio (262-190 a.c.) introdusse una definizione unitaria di superficie
conica, descritta da una retta che, passando per un punto collocato su un
piano esterno ad una circonferenza “percorre” i punti della circonferenza
![]()
|
|
|