Guide rettilinee

Come si può pilotare il moto rettilineo di un punto senza ricorrere alla predeterminazione fisica della traiettoria, come accade quando si disegna un segmento con l’utilizzo di una riga? L'interesse del problema non è solo teorico ed ha impegnato ingegneri e matematici alla fine del ‘700 e in parte dell'800, motivato dalla ricerca di un sistema utile per guidare l'asta del pistone di una macchina a vapore in un moto rettilineo alternato.

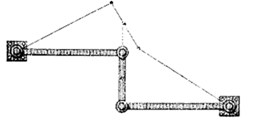
Nel 1784 James Watt, l'inventore della macchina a vapore, ottenne una soluzione approssimata del problema: in determinate condizioni il punto centrale del braccio di connessione si muove in un modo tale da discostarsi minimamente da una linea retta, ma studiando il meccanismo si può osservare che tale punto descrive un arco di una curva di sesto grado.

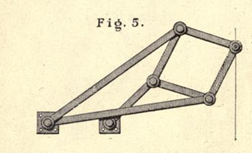
Altre soluzioni approssimate vennero trovate successivamente, ma la soluzione esatta venne fornita da Peaucellier nel 1864 e da Lipkin nel 1871, con un meccanismo che utilizza le proprietà della inversione circolare (particolare corrispondenza fra i punti di un piano). La soluzione di Peaucellier passò inosservata, proprio in un periodo in cui eminenti geometri dubitavano che tale soluzione esistesse finché Lipkin giunse alla stessa soluzione, ricevendo anche una ricompensa dal suo governo.

Alcuni meccanismi che forniscono la soluzione del problema furono trovati successivamente da Kempe (1876) a da altri matematici.