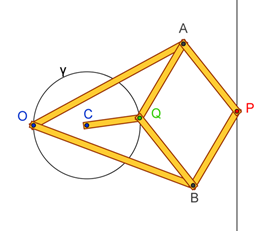
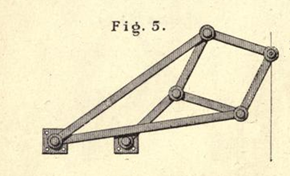
Guida rettilinea di Peaucellier
|
|
|
|
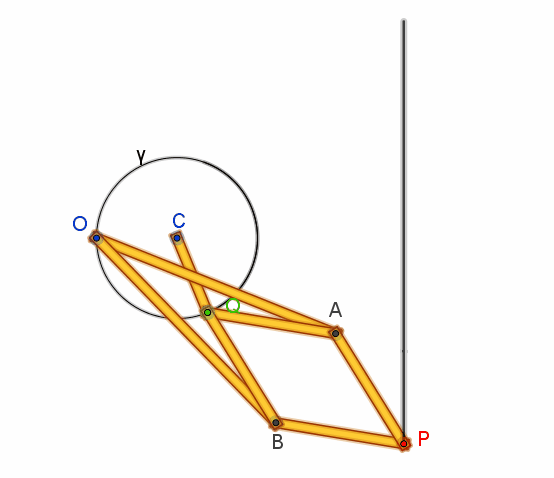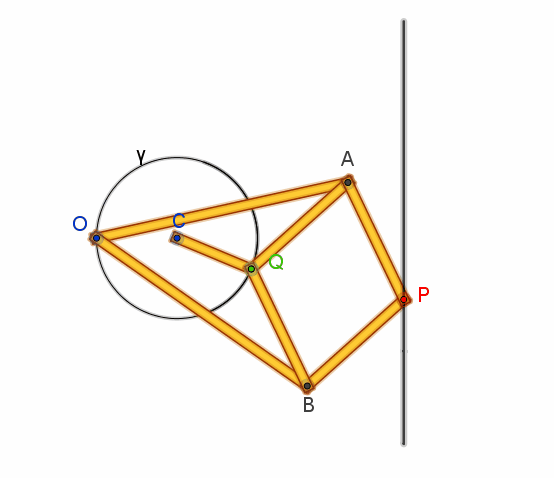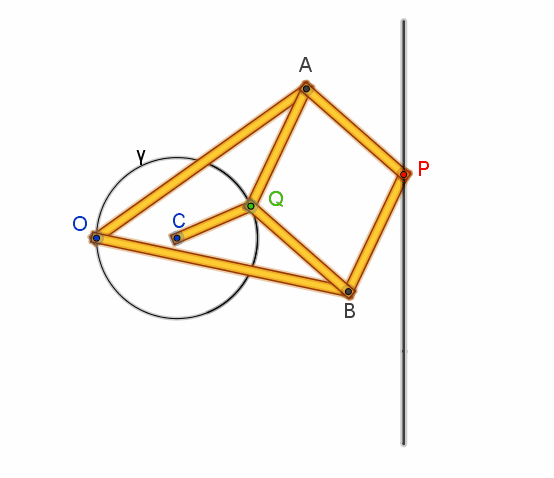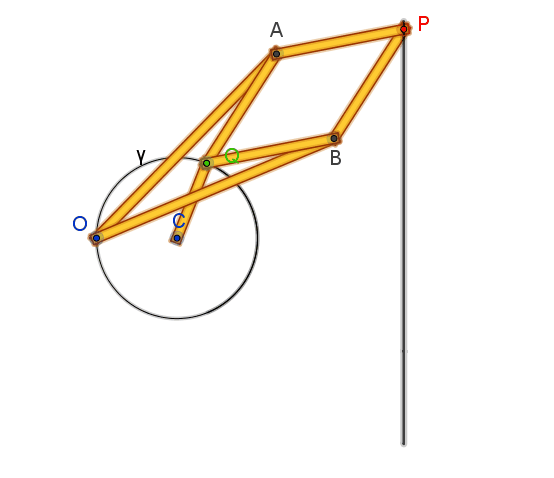
Due aste di uguale
lunghezza OA = OB = a hanno uno dei loro estremi imperniato al punto fisso O:
gli altri due estremi sono incernierati ai vertici opposti A e B di un rombo articolato APBQ con lati AP
= PB = BQ = QA = b< a.
Si dimostra che il
prodotto OP × OQ è costante, quindi P e Q
si corrispondono in una inversione circolare, particolare trasformazione
quadratica dei punti del piano.
Se allora Q è costretto
da una manovella fissata in C a descrivere una circonferenza passante per O, le
proprietà dell’inversione ci garantiscono che il punto P traccerà una retta.
![]()