 Mesolabio
Mesolabio
Lo strumento è legato al problema della
duplicazione del cubo, che fu ridotto da Ippocrate da Cnio
al problema di cercare due segmenti medi proporzionali fra due segmenti dati a
e b. Infatti dalle equazioni a:x=x:y=y:b
si ricava x3 =a2b
che per b=2a diviene x3 =2a3.
Il problema non è risolubile con riga e compasso. Il mesolabio consente di
reperire per via meccanica due medi proporzionali fra due segmenti assegnati.
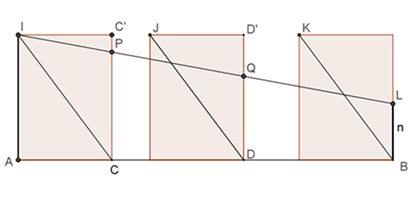
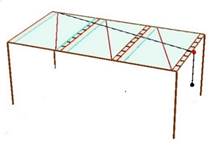
![]() Lo
strumento è costituito da tre tavolette rettangolari uguali e scorrevoli l’una
sull’altra. Un filo, teso per gravità da una massa sospesa ad uno dei suoi
estremi, congiunge i punti I e L. Siano
P e Q i punti di intersezione del filo con i lati CC’ e DD’ delle prime
tavolette. Le tavolette vengono spostate in modo tale che P si trovi
sulla diagonale JD e Q sulla diagonale KB. I segmenti PC e QD così ottenuti
soddisfano la relazione: AI:PC=PC:QD=QD:LB
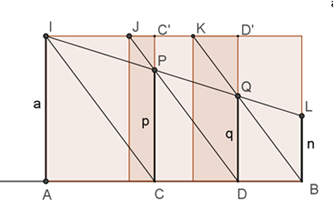
Lo
strumento è costituito da tre tavolette rettangolari uguali e scorrevoli l’una
sull’altra. Un filo, teso per gravità da una massa sospesa ad uno dei suoi
estremi, congiunge i punti I e L. Siano
P e Q i punti di intersezione del filo con i lati CC’ e DD’ delle prime
tavolette. Le tavolette vengono spostate in modo tale che P si trovi
sulla diagonale JD e Q sulla diagonale KB. I segmenti PC e QD così ottenuti
soddisfano la relazione: AI:PC=PC:QD=QD:LB
|
|
|