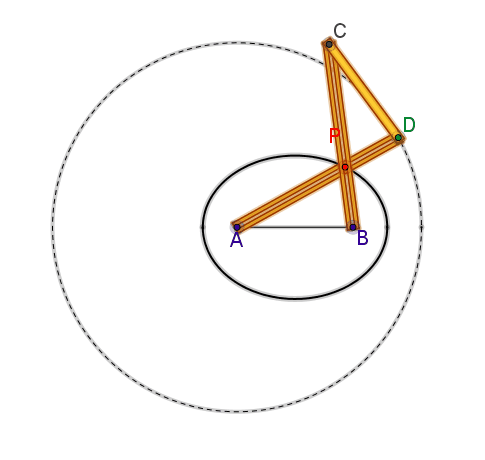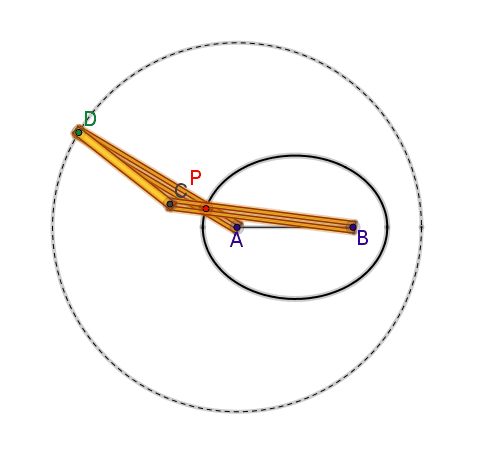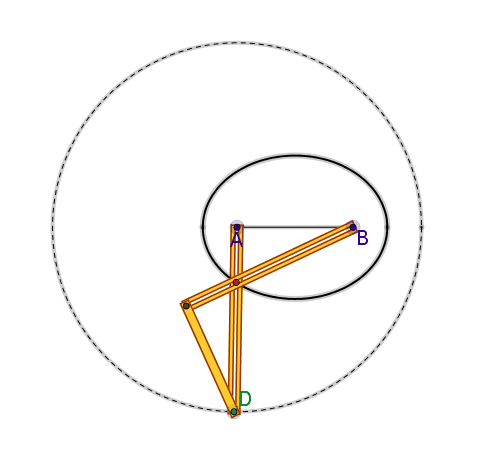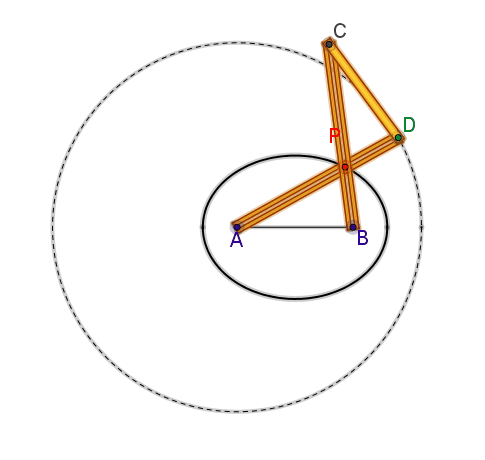
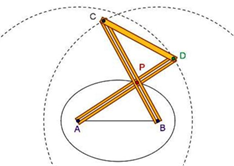
Si chiama antiparallelogramma articolato un quadrilatero (piano) articolato ABCD due lati opposti del quale (AB, CD) sono i lati non paralleli di un trapezio isoscele, mentre gli altri due lati (AD, BC) sono le diagonali del trapezio.

Collochiamo l’antiparallelogramma su un piano π; supponiamo di bloccare su π una delle aste più corte (per esempio AB: fissando un perno in A e un altro in B), e muoviamo l’asta AD.

Si può facilmente constatare che i punti C e D percorrono le circonferenze aventi centro, rispettivamente, in A e B. I lati AD e BC dell’antiparallelogramma, si incontrano in P.

Risulta PA + PB = PA + PD = AD = cost. (poiché l’antiparallelogramma ha un asse di simmetria a cui appartiene P). Perciò il luogo descritto da P è una ellisse con fuochi in A e in B e asse maggiore di lunghezza uguale ad AD.