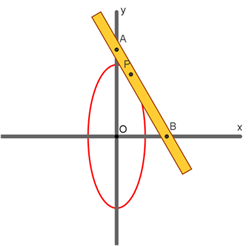
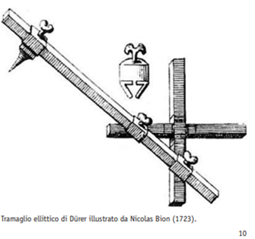
Ellissografo di Proclo
|
|
|
|
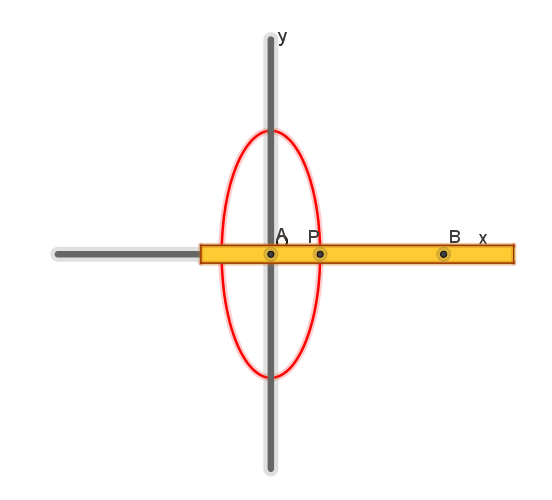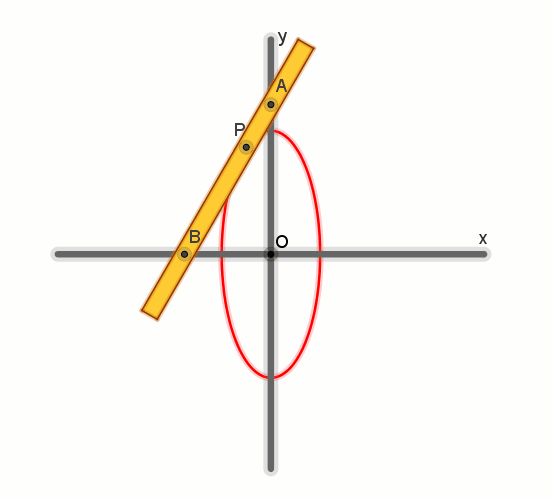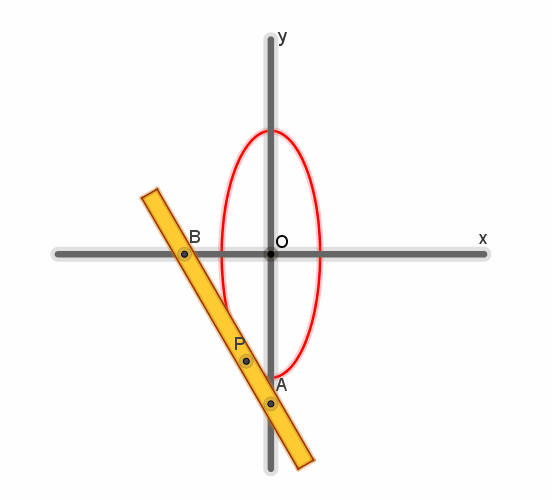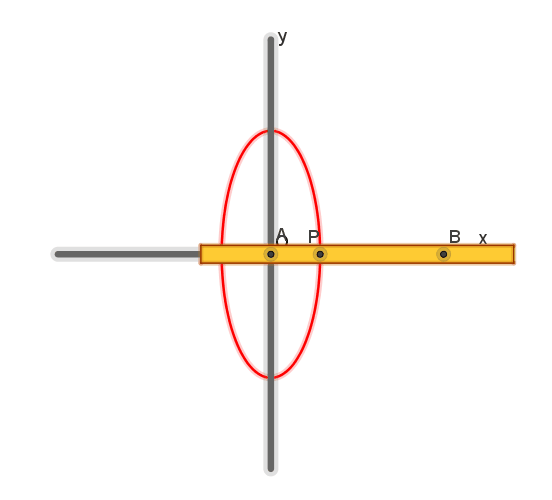
A Proclo è attribuito il
teorema secondo il quale se un segmento di data lunghezza si muove mantenendo i
suoi punti estremi su due rette che si intersecano, un punto giacente sul
segmento descriverà una porzione di ellisse
Un’asta rettilinea (di
legno o metallo) può ruotare attorno a due perni A e B vincolati ad essa in
modo che la distanza AB sia costante. I perni sono sorretti da cursori
obbligati a scorrere entro guide rettilinee ortogonali x, y (che si intersecano
in O). Una punta scrivente P può essere bloccata sull’asta in un qualsiasi
punto di essa (quindi AP è costante).
Quando A e B scorrono
lungo x e y, P descrive una ellisse con assi di simmetria coincidenti con le
guide ortogonali e semiassi di lunghezza PA e PB.
![]()