Parabolografo del Cavalieri

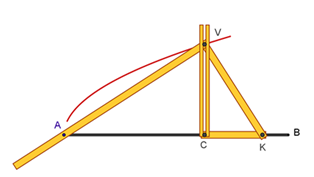Questa macchina incorpora, come propria legge il "sintomo" di Menecmo: ma ne altera profondamente la percezione teorica. Infatti la proporzione di Menecmo perde qui il carattere di verità statica, da contemplare dentro a un oggetto dato: diviene "operante", governa la macchina, costruisce la conica.

Inoltre è una proprietà attiva nel piano in quanto ogni legame della curva col cono di sostegno è eliminato (il lato retto è qui la distanza fissa tra due punti del telaio mobile). Strumenti di questo tipo mettono in evidenza come i diversi punti della curva devono essere posizionati in un piano rispetto a un sistema di riferimento (parti fisse del meccanismo) che può essere scelto ad arbitrio: producono quindi e rafforzano alcune schematizzazioni astratte necessarie alla costruzione futura della identità curva-equazione.

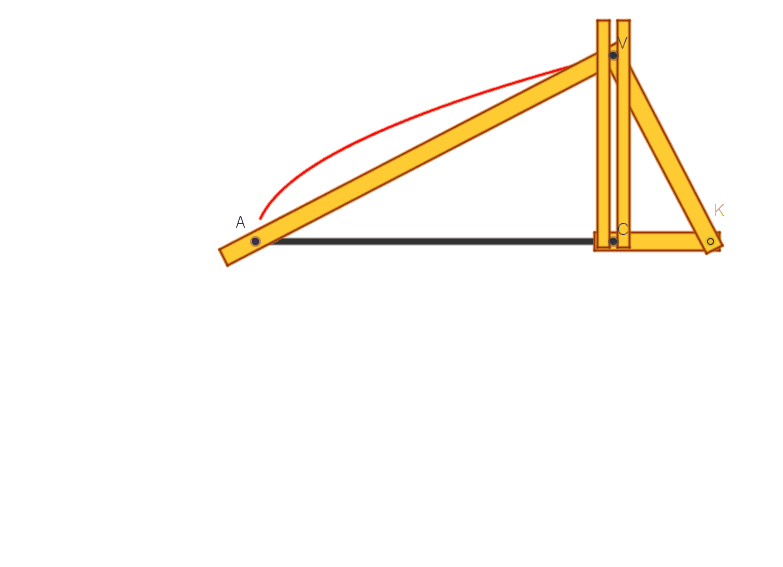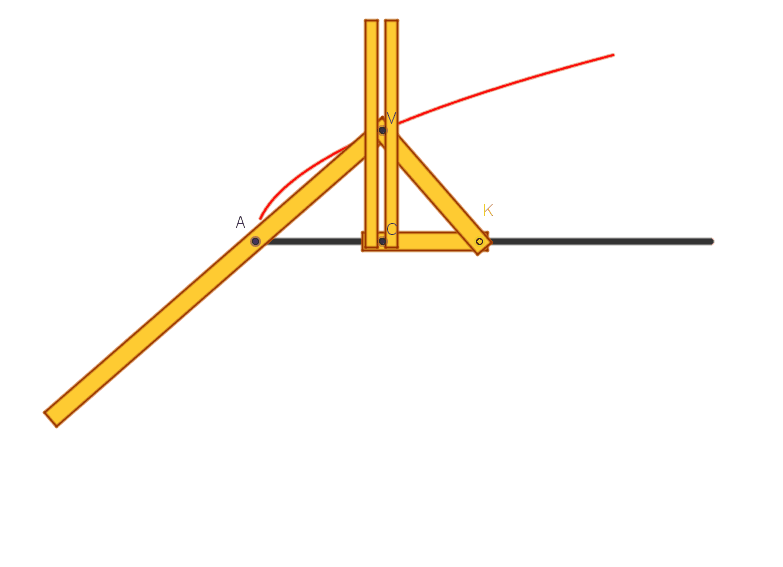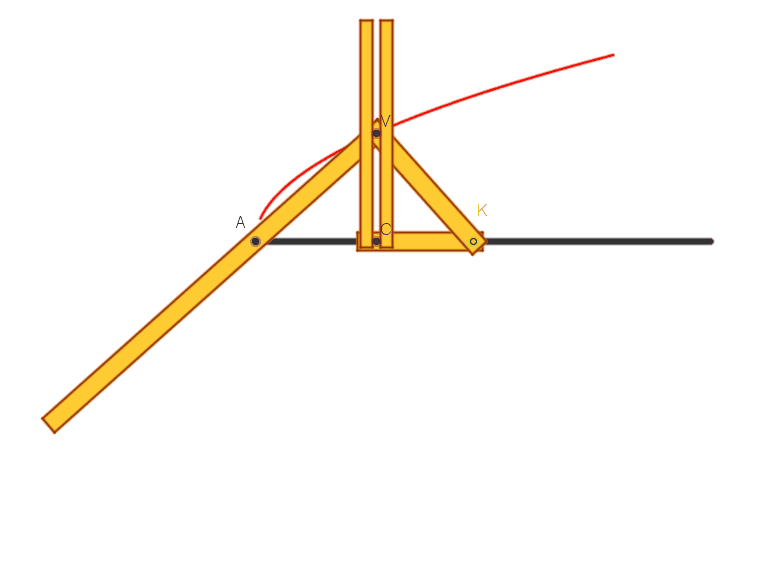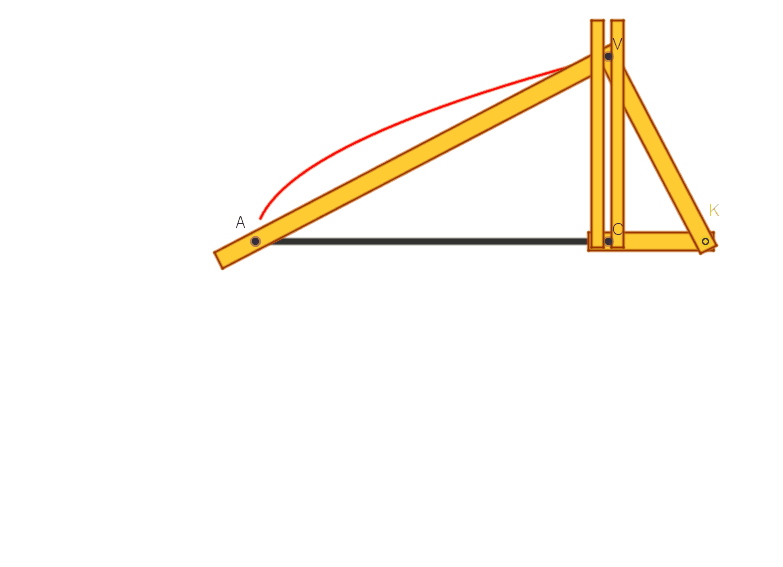
Lungo la scanalatura rettilinea AB praticata in un piano p scorre un segmento CK (materializzato in legno o metallo) di lunghezza k prestabilita. Al suo estremo C è vincolata rigidamente, in direzione perpendicolare a CK, una asta CV, giacente su p. Quando l’angolo retto KCV si muove, trascina con sé un altro angolo retto AVK (materializzato anch’esso in legno o metallo), che ha i lati VA e VK costretti a passare, rispettivamente, per i punti A e K.

Durante il movimento, in ogni istante AVK è un triangolo rettangolo (variabile) di cui VC rappresenta l’altezza relativa alla ipotenusa e AK l’ipotenusa. Possiamo applicare ad esso il teorema di Euclide: si ricava (VC´VC) = (CK´CA) = (k´CA), proprietà caratteristica della parabola (ponendo CA = x, VC = y, si scrive y²=kx).