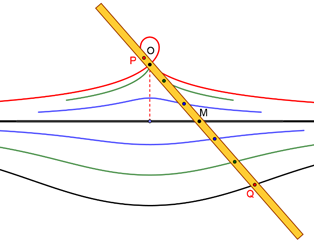
In un piano è praticata una fenditura rettilinea r e fissato un perno O (polo) a distanza OH=a da r. Nel piano individuato dalla retta r (curva base) e dal punto O si fa muovere un’asta s (realizzata in legno o metallo) in modo che essa sia costantemente vincolata a passare per O mentre un cursore M, fissato a un punto di s, scorre all’interno della scanalatura. Si collocano poi su s, a distanza b (intervallo) da M (e da parti opposte rispetto ad M) due tracciatori P e Q, che durante il movimento dell’asta disegnano la concoide.

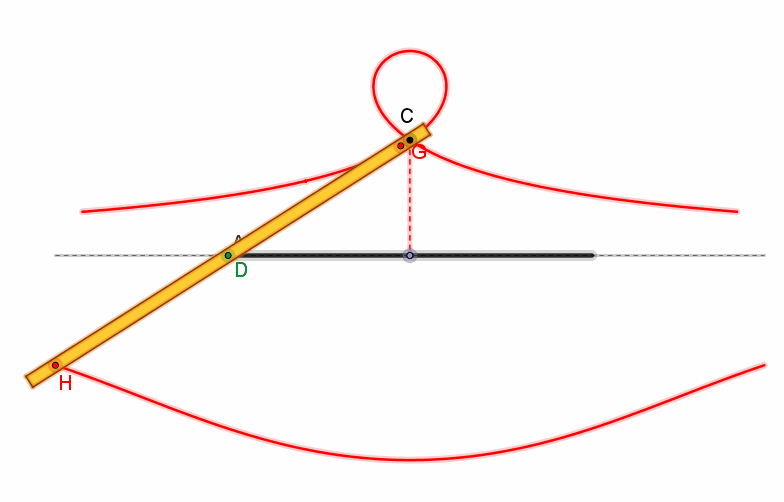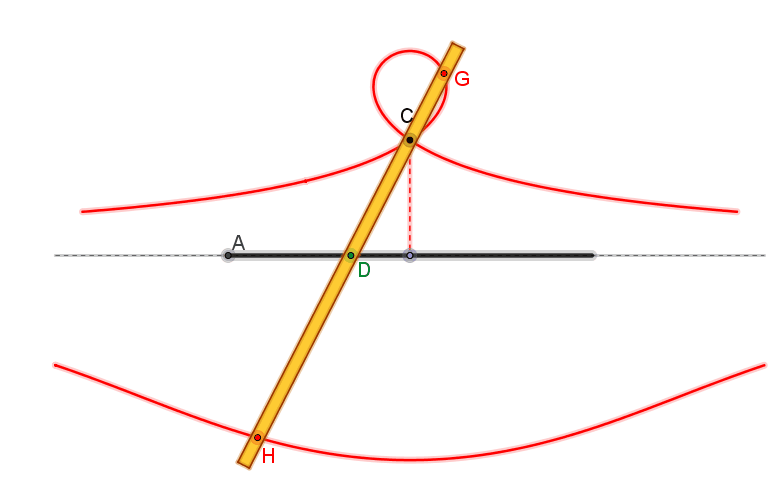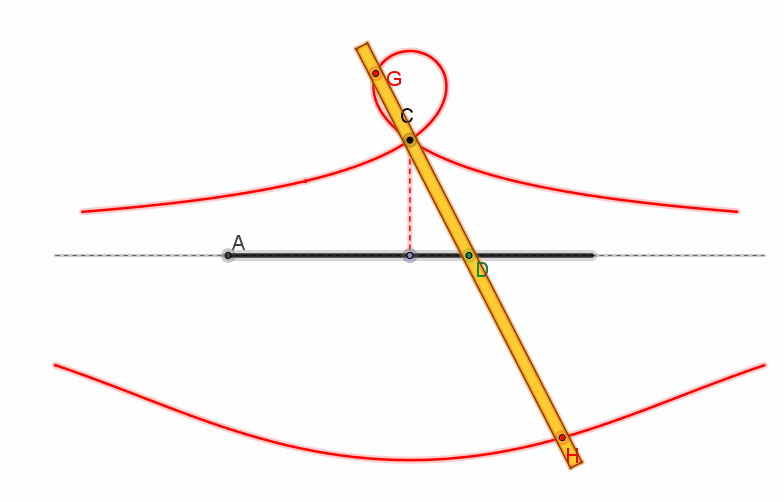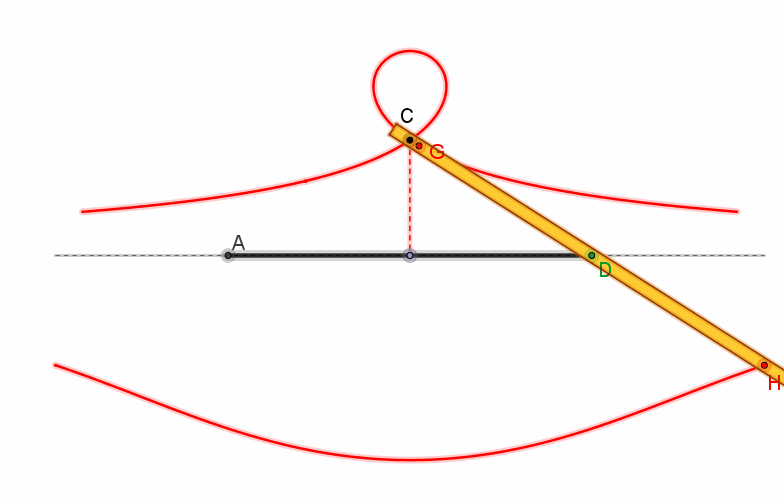
E’ una curva (caratterizzata da base, polo e intervallo) costituita da due rami, separati dalla retta r: l’aspetto del ramo che giace dalla parte in cui si trova O dipende dalla relazione tra l’intervallo b e la distanza OH = a. Precisamente, tale ramo presenta un nodo se b > a, una cuspide se b = a, un punto isolato se b < a.

La curva è celebre soprattutto per due ragioni: il meccanismo tracciatore, oltre ad essere semplice, è di elevata precisione; serve inoltre a risolvere problemi (duplicazione del cubo, trisezione dell’angolo) non affrontabili con riga e compasso.