|
|
|
|
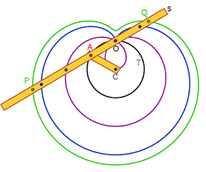
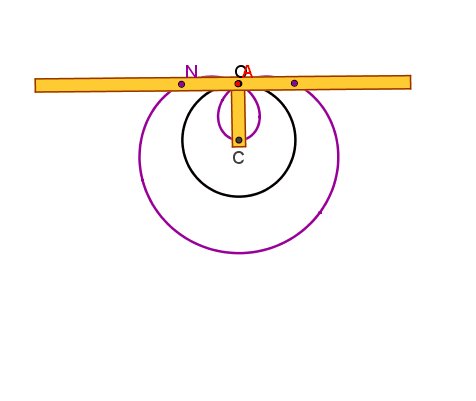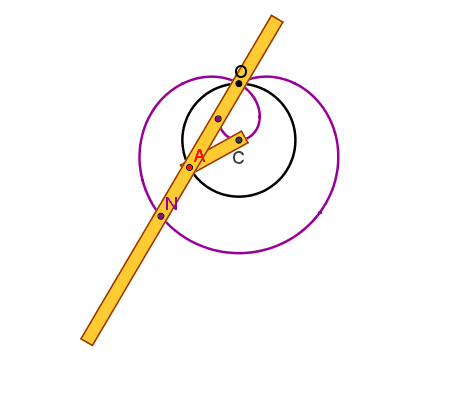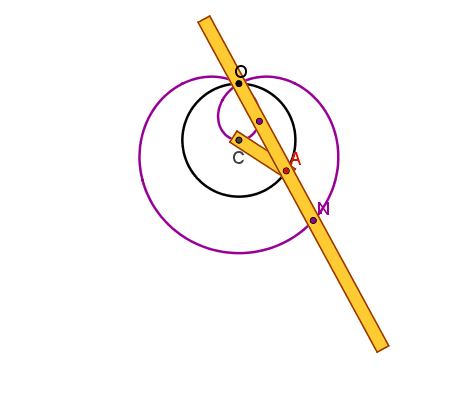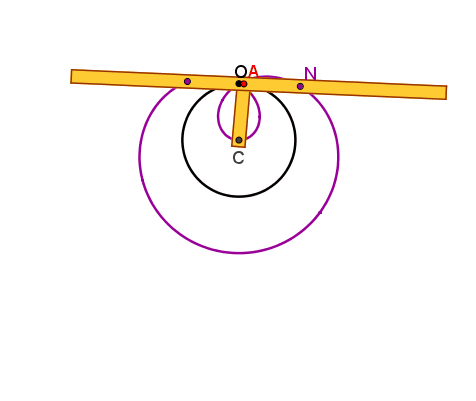
Lumache di Pascal
Il punto A è vincolato
dall'asta AC=r, imperniata al piano in C, alla circonferenza γ di raggio r. L'asta s, incernierata in A
alla CA , è vincolata a passare per un punto fisso O del piano, scelto sulla
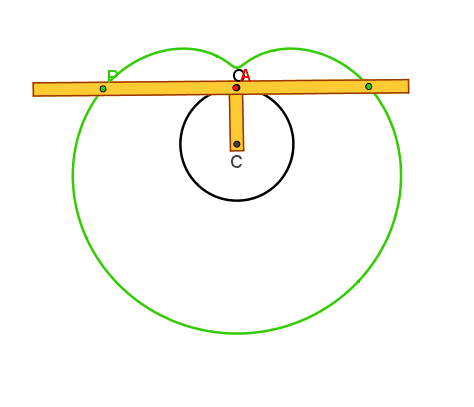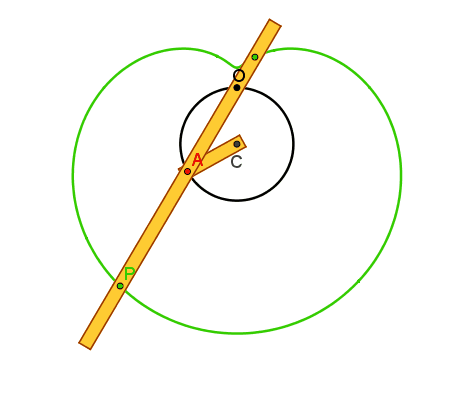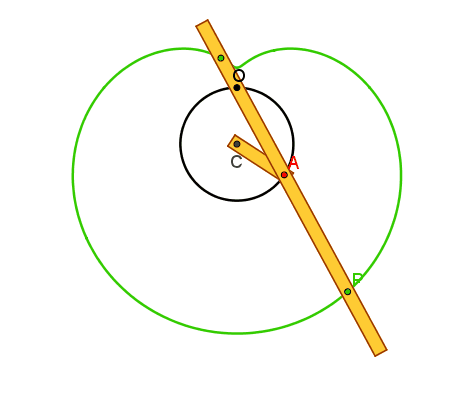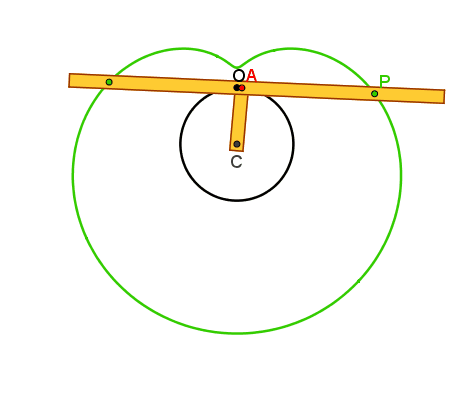
circonferenza γ. Quando A descrive γ ognuno dei punti P e Q
scelti su s in modo che siano simmetrici rispetto ad A, descrive una lumaca di
Pascal (concoide avente come curva base la circonferenza γ e polo O) , che presenta in O un punto doppio isolato, un nodo o una
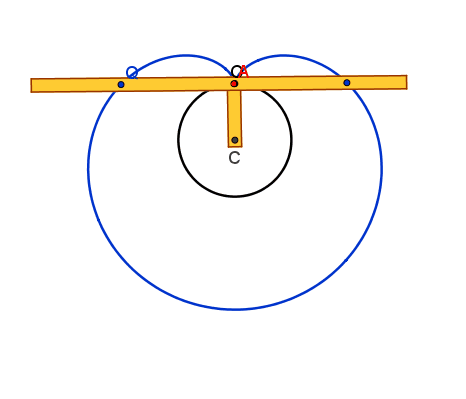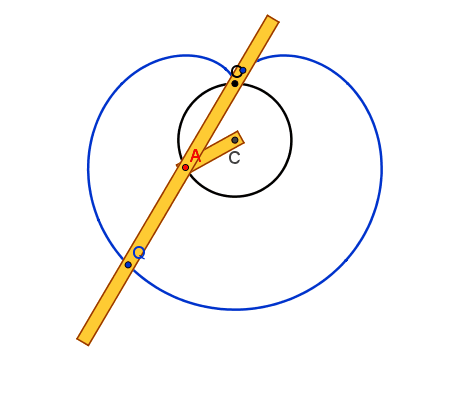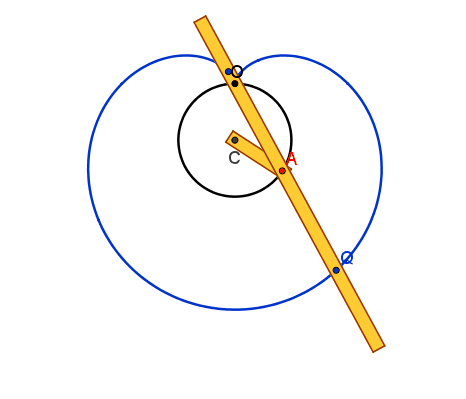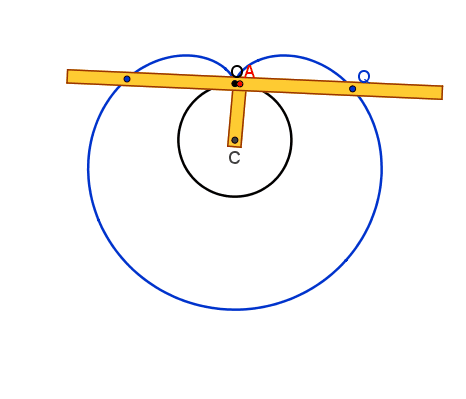
cuspide se risulta rispettivamente
AP>2r, AP<2r o AP=2r.
La curva era nota ai
geometri greci, in quanto concoide della circonferenza, ma prese il suo nome
solo nel ‘600. Dὒrer descrive un metodo per la sua costruzione nel
Underweysung der Messung…
La lumaca di Pascal,
fra le numerose proprietà ha quella di essere una curva trisettrice.
![]()
|
|
|
|