Compasso perfetto.

I compassi "perfetti" (detti così perchè possono tracciare sia circonferenze che archi di sezioni coniche qualsiansi) hanno una probabile origine araba (X-XII secolo).

Nel periodo rinascimentale ne furono costruiti diversi esempi, naturalmente con varianti tecniche e strutturali (ricordiamo quelli di F. Barozzi, di G.B. Benedetti, di G. Tiene). Anche Cartesio descrisse un compasso perfetto nelle “Cogitationes privatae”. Il modello qui riprodotto è simile allo strumento descritto da B. Cavalieri nello "Specchio Ustorio": Cavalieri scrive di averlo visto "appresso li Molto RR. PP. Gesuiti, qual mi dicono essere inventione e fabrica del P. Scheiner dell'istessa Compagnia". Si riconosce immediatamente che il congegno meccanizza in modo diretto la definizione di Apollonio: una delle aste è l'asse del cono; l'altra ne è una generatrice, e può allungarsi o accorciarsi per consentire il contatto continuo tra lo "stilo" e il piano del disegno (piano secante).

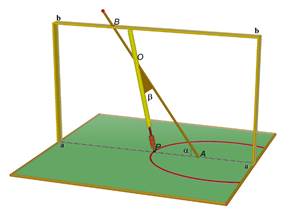
L’asse AB (girevole su sé stesso attorno ai cardini A e B) può essere inclinato di un angolo a variabile nel piano delle rette parallele aa, bb perpendicolare al piano su cui scorre il tracciatore P. Questo è sostenuto dall’asta OP, vincolata in O all’asta AB con la quale forma un angolo variabile b. Quando AB ruota, OP descrive un cono di asse AB: il tracciatore P è mantenuto a contatto col piano del disegno (un giunto "telescopico" permette all’asta OP di accorciarsi o allungarsi) il quale "taglia" il cono generando la sezione descritta da P. Se a = b si ha una parabola, se a > b una ellisse (circonferenza se a = p/2 > b), se a < b una iperbole

animazione

A cura dell'Associazione Macchine Matematiche