Le macchine di Cartesio
 Con Cartesio la
cultura aritmetico-algebrica (sviluppatasi con il diffondersi dell’economia
mercantile) e la geometria si unificano: un problema geometrico deve essere
tradotto in una equazione, le cui radici devono essere costruite con mezzi
accettabili. Le “curve da costruzione”, utilizzate per risolvere problemi, non
sono più solamente rette e coniche, ma curve tracciate con moto continuo da
meccanismi di vario tipo.
Con Cartesio la
cultura aritmetico-algebrica (sviluppatasi con il diffondersi dell’economia
mercantile) e la geometria si unificano: un problema geometrico deve essere
tradotto in una equazione, le cui radici devono essere costruite con mezzi
accettabili. Le “curve da costruzione”, utilizzate per risolvere problemi, non
sono più solamente rette e coniche, ma curve tracciate con moto continuo da
meccanismi di vario tipo.
Esse possono essere accettate e usate
nel discorso teorico, purché soddisfino ad alcune condizioni: le curve devono
essere generate mediante movimenti continui di rette che si intersecano,
movimenti concatenati in modo che i seguenti sono interamente determinati dai
precedenti e in ogni istante si possa avere una conoscenza esatta dei loro
rapporti. L’utilità e la fecondità della figura strumentale non stanno tanto
nella costruzione meccanica come tale, quanto nel principio di verità che essa
contiene un principio di ordine: passaggi successivi perfettamente determinati
l’uno dall’altro, con un rigoroso controllo delle misure e delle relazioni che
li legano reciprocamente.
Mentre le macchine descritte nella sua
“Geometria” sono strumenti concettuali che servono a classificare le curve,
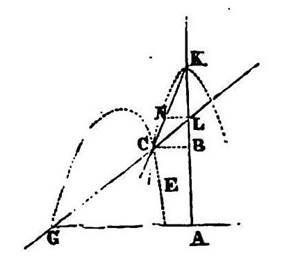
nella “Diottrica” sostiene
…è necessario inventare qualche altro
strumento per mezzo del quale sia possibile descrivere iperboli di un sol
tratto, come si descrivono cerchi con un compasso. E non ne conosco alcuno
migliore del seguente….
![]() di cui dà una
descrizione ricchissima di particolari ad uso dei costruttori.
di cui dà una
descrizione ricchissima di particolari ad uso dei costruttori.