L’ultimo strumento esposto (sezioni del toro) collega la geometria greca alla geometria delle trasformazioni: le sezioni del toro, studiate per primo da Perseo nel II sec. a.C. vengono tracciate nel piano (in un caso particolare) da un biellismo che realizza una trasformazione geometrica non lineare.

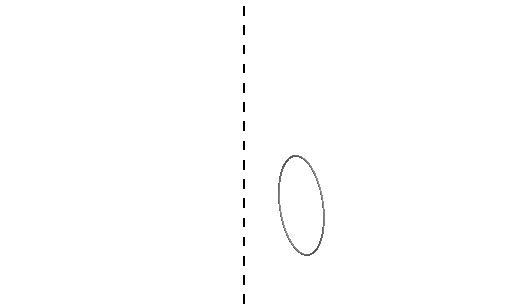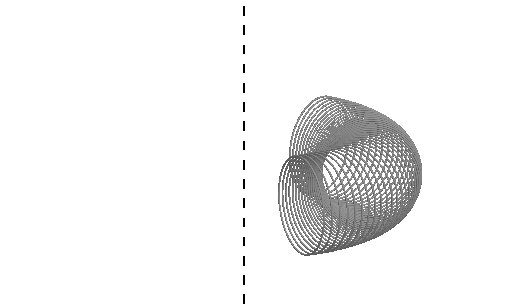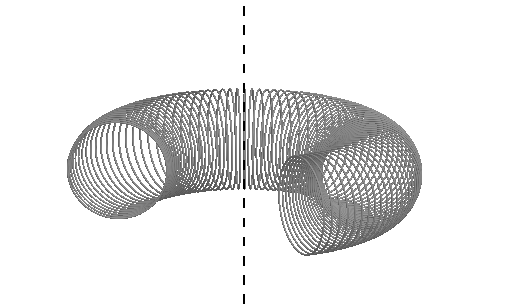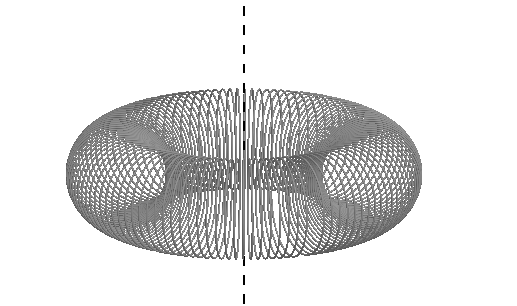
Le sezioni del toro vennero studiate dal matematico Perseo (II sec a.C.).

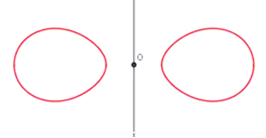
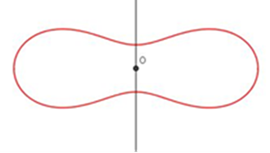
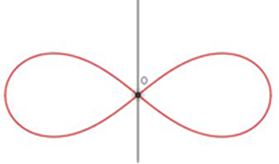
Il toro è la superficie generata dalla completa rotazione di un cerchio attorno ad una retta tracciata ad arbitrio nel suo piano. Vi sono tre tipi di tori perché parametri che lo caratterizzano sono due: il raggio r del cerchio generatore, la distanza d tra il centro di tale cerchio e l’asse di rotazione. Sezionando il toro con un piano parallelo all’asse di rotazione si ottengono le “spiriche”, la cui forma varia con la distanza p del piano secante dall’asse di rotazione. Nel modello si possono riconoscere le spiriche (ovali del Cassini) ottenute sezionando un toro aperto, costituite da:

Due ovali, una esterna all’altra

p<d-r

Una sola ovale

d-r<p<d+r

una curva con un punto doppio

p=d-r