
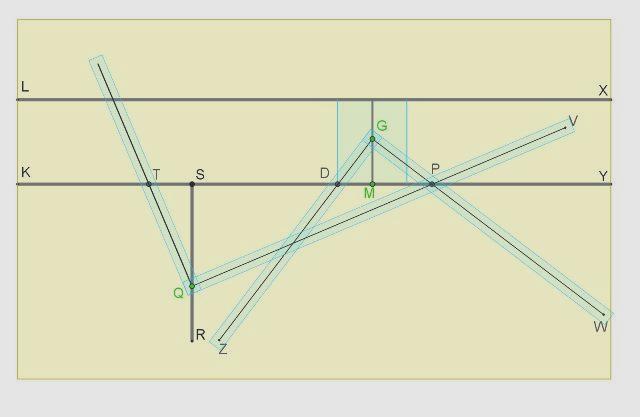
Risoluzione della equazione x³ + px = q .
Sul piano sono praticate tre scanalature rettilinee: LX, KY (parallele), SR (perpendicolare alle precedenti). Un cursore rettangolare ABCD, che trasporta una quarta scanalatura MN (parallela a SR e praticata in modo che sia DM=1), scivola avanti e indietro guidato da LX, KY. Una squadra TQV ha il vertice Q che può essere fissato in un punto qualsiasi della scanalatura SR; una seconda squadra ZGW ha il vertice G scorrevole entro MN e il lato GZ costretto a passare per D. Si fissi Q in modo che , ed M in una posizione tale da avere SM=p. Infine, si faccia ruotare la squadra TQV attorno a Q e si muova ZGW in modo che siano realizzate le due seguenti condizioni: 1) i lati QV e GW si incontrino in un punto P appartenente a KY; 2) Sia TS = GM. Indicata con x la comune lunghezza di questi due ultimi segmenti, l'equazione risulta soddisfatta.


