Premessa:

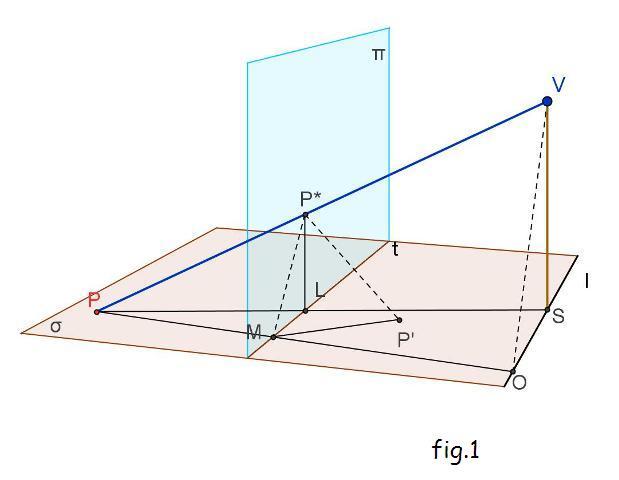
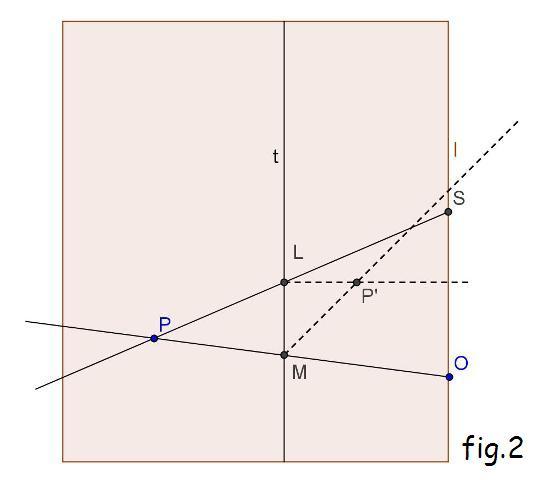
 In figura 1 siano: σ e π piani prospettivi; V  il punto di vista; P* l'immagine di P; t linea di terra; l retta limite; S ed L (rispettivamente) proiezioni ortogonali di V  e di P’ su σ. Proiettiamo V e P*  in O e M da un centro improprio con raggi paralleli a π e inclinati di 45° su σ; M ed O sono allineati con P (anche L ed S sono allineati con P). Proiettiamo P* in P’ con un raggio inclinato di 45° rispetto a σ e π (e contenuto in un piano perpendicolare a t, in modo tale che P e P’ siano da parti opposte rispetto a t (quindi LMP’ è un triangolo isoscele). La configurazione così ottenuta su σ (visibile in pianta nella figura 2) è quella realizzata da prospettografo di Lambert

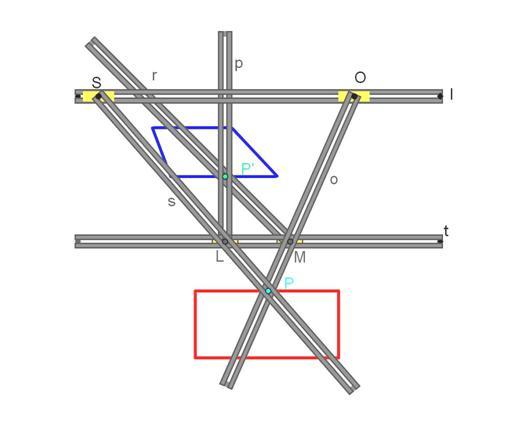
Nel prospettogafo di Lambert (1° modello) due aste scanalate parallele fra loro (t ed l) sono appoggiate sul piano; S ed O sono due perni fissati sulla l; o, p r, s sono aste dotate di scanalatura rettilinea così disposte:

• s è imperniata in S e costretta a passare per L, cursore scorrevole nella t

• o è imperniata in O e costretta a passare per M, cursore scorrevole nella t

• p è fissata al cursore L in modo tale da rimanere sempre perpendicolare a t

• r è fissata ad M in modo tale da formare sempre (durante la deformazione dello strumento) un angolo di 45° con t

Preso un punto P del piano di appoggio facciamo passare per esso le scanalature s ed o: il punto P’, intersezione delle aste r e p, è l’immagine prospettica di P.

 Esplora la macchina      Approfondimenti