
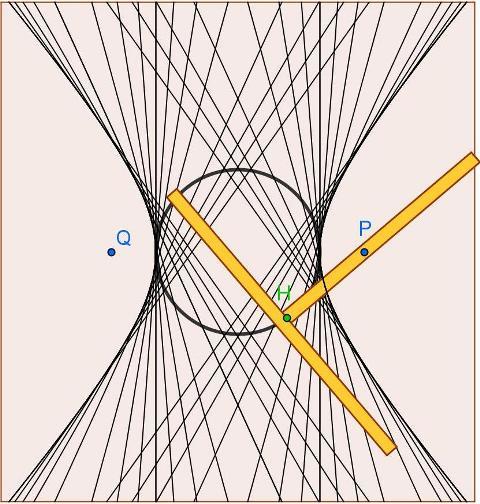
Il modello fisico illustra il teorema seguente:
La podaria di uno dei fuochi d’una iperbole rispetto alla iperbole stessa è la circonferenza avente come diametro l’asse principale della curva.
Quindi, facendo scorrere il vertice di un angolo retto lungo una circonferenza mentre uno dei suoi lati è costretto a passare per un punto fisso P esterno alla circonferenza, l’altro lato inviluppa una iperbole avente come asse principale il diametro della circonferenza utilizzata (e come fuoco il punto P).
Caso dell'angolo generico

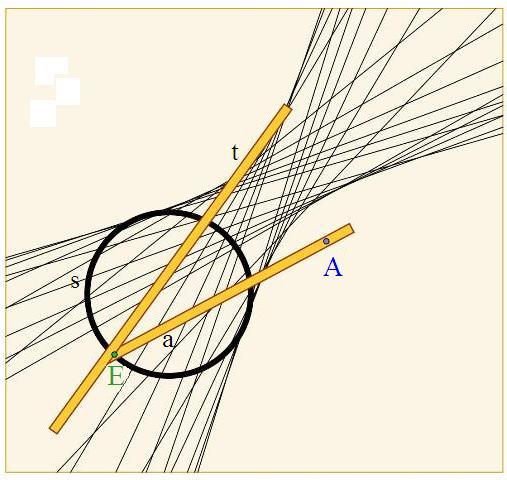
Lo strumento, è formato da due aste rigide aE e Et saldate insieme in modo da formare un angolo β di ampiezza prefissata (≠ π/2). L’asta aA (scanalata) è costretta a passare per il perno fisso A mentre il vertice E dell’angolo β percorre una scanalatura circolare s di centro C (delimitante un cerchio a cui A è esterno).
approfondimenti
Quando E si muove lungo s la retta Et inviluppa (nel piano di s) una iperbole
Metodo della polare

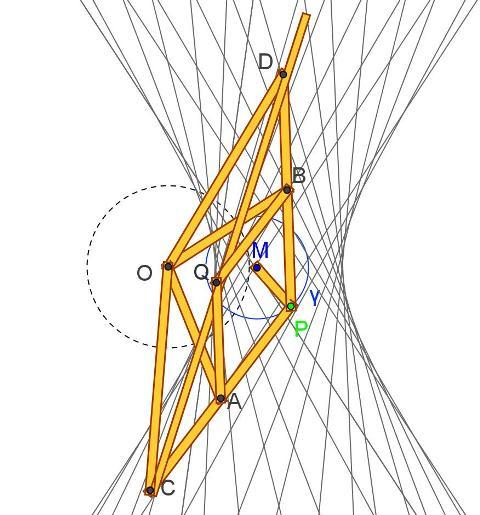
OA QBP è un inversore di Peaucellier, i punti A e B sono i punti medi delle aste PCe PD.Il punto P mediante l'asta PM è vincolato a percorrere la circonferenza γ di centro M e di raggio r2-AP2) inviluppa una iperbole.
Dimostrazione (pdf)
Metodo della corrispondenza
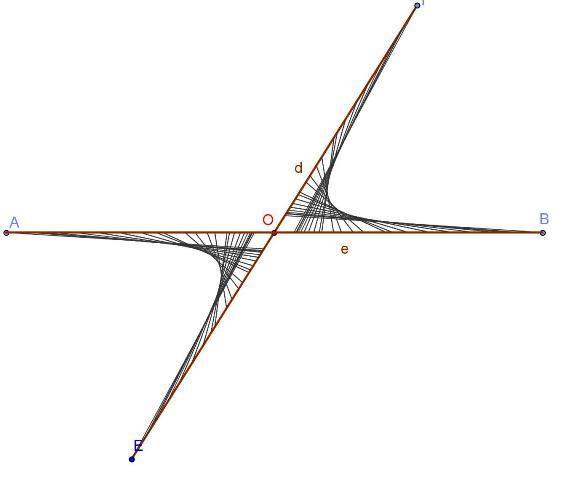
Tra i punti x’ e x di due punteggiate r ed r’ – materializzate nel modello fisico da aste di legno che possono ruotare (nel piano da esse individuato) l’una rispetto all’altra attorno al punto O (origine dei sistemi di riferimento)– è stabilita una corrispondenza definita dalla relazione x^'×x=k (*) con k = 80.
Congiungendo i punti corrispondenti con rette (materializzate da fili tesi) si ottiene una iperbole.


