Su 
si corrispondono il cerchio 
di base del cono (luogo dei punti P) e la corona circolare di centro O, raggio interno 
e raggio esterno 
(luogo dei punti Q).Poiché
, d’ (d: raggio luminoso uscente dalla sorgente S, incidente sullo specchio in A; d¢: raggio riflesso; : normale allo specchio in A) appartengono al piano passante per A e per l’asse del cono , se ne deduce che, in ogni posizione, i punti P e Q sono allineati con O. Inoltre, siccome
l’angolo di incidenza è uguale all’angolo di riflessione si ha: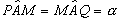 
; è anche 
, 
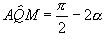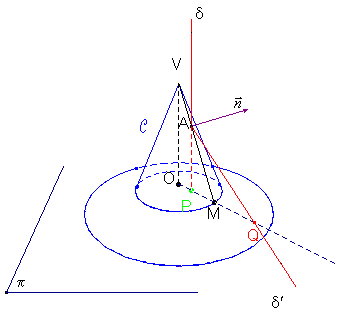
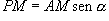(PAM è un triangolo rettangolo).
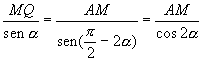(teorema dei seni applicato al triangolo QAM).
Quindi 
. Fissato sul piano p un sistema di coordinate polari avente come polo O e come asse polare un (qualsiasi) raggio uscente da O, indicate con 
e 
le coordinate di P e con 
’ e ’ le coordinate di Q, si ha: 
(P e Q sono allineati con O) 
; allora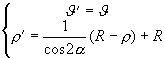 
sono le equazioni della corrispondenza in coordinate polari.