Ellissografo del Delaunay

Fig.1

Fig.2

Fig.3

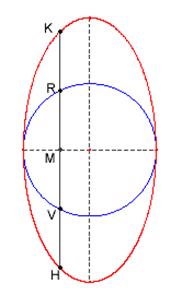
Teorema: Se una corda HK parallela all’asse principale a di una ellisse incontra la circonferenza che ha per diametro l’asse secondario b in due punti V ed R, il rapporto tra le due corde HK ed RV è costante ( si ha ).

Ovviamente è anche (cfr. fig.1) : .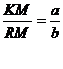

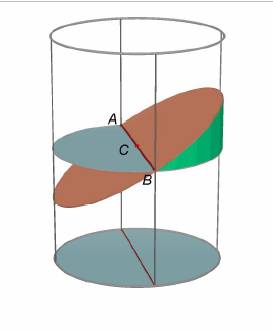
Questa proprietà, già nota ad Archimede, si dimostra facilmente ricordando che ogni ellisse si può ottenere come sezione piana di un cilindro rotondo avente come diametro del cerchio di base l’asse secondario dell’ellisse considerata. Un esempio è fornito in fig.2, dove AB è asse del cerchio di base e contemporaneamente asse dell’ellisse sezione.

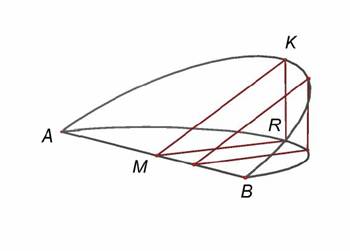
Estraendo dal cilindro lo “spicchio” rappresentato in fig.3, si vede subito che le sue intersezioni KMR con i piani perpendicolari ad AB sono triangoli rettangoli tutti simili tra loro e che, di conseguenza cost.

La proprietà incorporata nel meccanismo del Delaunay (la costante è il rapporto k delle distanze dei punti P e Q dalla scanalatura) ci assicura che la curva tracciata da Q è ottenuta dilatando, nel medesimo rapporto k, le corde della circonferenza (descritta da P) perpendicolari alla scanalatura: tale curva è dunque una ellisse.

Occorre segnalare che:

· la forma dell’ellisse tracciata da Q dipende dal modo in cui sono scelti su PC e PB i punti S e T,

· la sua posizione nel piano di pende dalla posizione di O

· le sue dimensioni dipendono dalla lunghezza della manovella.

Utilizzando manovelle di diversa lunghezza la macchina traccerà ellissi tutte simili fra loro, essendo costante (sempre uguale a k) il rapporto fra le lunghezze dei loro semiassi.

Fig.1

Fig.1